题目内容
18.某行星的一颗小卫星在半径为r的圆轨道上绕该行星运动,运行时的周期是T.已知引力常量为G,求这个卫星的线速度及该行星的质量M.分析 根据线速度与周期、半径的关系即可求出线速度;卫星在转动中,万有引力提供向心力,则由万有引力公式可求得行星的质量.
解答 解:线速度的大小等于卫星转过的弧长与时间的比值,即:v=$\frac{l}{t}$=$\frac{2πr}{T}$.
设卫星质量为m,由万有引力定律,得:${F}_{向}=\frac{GMm}{{r}^{2}}$…①
由匀速圆周运动性质,得:T=$\frac{2π}{T}$…②
又:${F}_{向}=m{ω}^{2}r$…③
由①②③得:M=$\frac{4{π}^{2}{r}^{3}}{G{T}^{2}}$
答:这个卫星的线速度是$\frac{2πr}{T}$,该行星的质量是$\frac{4{π}^{2}{r}^{3}}{G{T}^{2}}$.
点评 求天体的质量时,只能求中心天体的质量;因已知卫星的周期,故向心力公式选择.

练习册系列答案
相关题目
10.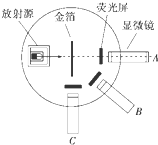 如图所示为卢瑟福和他的同事们做α粒子散射实验的装置示意图,荧光屏和显微镜一起分别放在图中的A、B、C三个位置时,关于观察到的现象,下列说法中正确的是( )
如图所示为卢瑟福和他的同事们做α粒子散射实验的装置示意图,荧光屏和显微镜一起分别放在图中的A、B、C三个位置时,关于观察到的现象,下列说法中正确的是( )
 如图所示为卢瑟福和他的同事们做α粒子散射实验的装置示意图,荧光屏和显微镜一起分别放在图中的A、B、C三个位置时,关于观察到的现象,下列说法中正确的是( )
如图所示为卢瑟福和他的同事们做α粒子散射实验的装置示意图,荧光屏和显微镜一起分别放在图中的A、B、C三个位置时,关于观察到的现象,下列说法中正确的是( )| A. | 相同时间内放在A位置时观察到屏上的闪光次数最少 | |
| B. | 相同时间内放在B位置时观察到屏上的闪光次数最少 | |
| C. | 相同时间内放在C位置时观察到屏上的闪光次数最少 | |
| D. | 放在C位置时观察不到屏上有闪光 |
7.在万有引力的发现过程中,许多的物理学家做出了积极的贡献,其中最早在实验室中测量出引力常量的科学家是( )
| A. | 牛顿 | B. | 伽利略 | C. | 卡文迪许 | D. | 开普勒 |
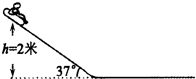 如图所示,一滑雪场有一倾角为37°的雪坡,雪坡上的雪道与水平雪道相连.一个人坐在玩具雪橇里从雪坡上高2m处由静止开始自由滑下,雪橇与雪道的动摩擦因数为0.075.(g=10m/s2,sin37°=0.6,cos37°=0.8)求:
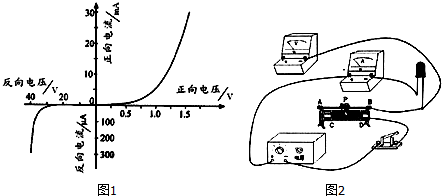
如图所示,一滑雪场有一倾角为37°的雪坡,雪坡上的雪道与水平雪道相连.一个人坐在玩具雪橇里从雪坡上高2m处由静止开始自由滑下,雪橇与雪道的动摩擦因数为0.075.(g=10m/s2,sin37°=0.6,cos37°=0.8)求: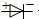 ”,且具有单向导电性,即电流从正极流入时电阻比较小,而从负极流入时电阻比较大.厂家提供的伏安特性曲线如图1.某兴趣小组测绘施加反向电压时的伏安特性曲线,以验证与厂家提供的数据是否一致,可选用的器材有:
”,且具有单向导电性,即电流从正极流入时电阻比较小,而从负极流入时电阻比较大.厂家提供的伏安特性曲线如图1.某兴趣小组测绘施加反向电压时的伏安特性曲线,以验证与厂家提供的数据是否一致,可选用的器材有: