题目内容
4. 如图所示,把一个质量m=0.2kg的小球从h=7.2m的高处以60°角斜向上抛出,初速度v0=5m/s,不计空气阻力,重力加速度g=10m/s2.问:
如图所示,把一个质量m=0.2kg的小球从h=7.2m的高处以60°角斜向上抛出,初速度v0=5m/s,不计空气阻力,重力加速度g=10m/s2.问:(1)从抛出到落地过程中重力对小球所做的功W是多少?
(2)小球落地时速度的大小v是多少?
分析 (1)重力做功根据公式W=mgh,h是初末位置的高度差.
(2)根据动能定理或机械能守恒定律求出小球落地时的速度大小.
解答 解:(1)由于不计空气阻力,小球在运动过程中只有重力做功,机械能守恒.
重力对小球所做的功:WG=mgh=0.2×10×7.2J=14.4J
(2)由动能定理有:mgh=$\frac{1}{2}m{v}^{2}$-$\frac{1}{2}m{v}_{0}^{2}$
解得:v=$\sqrt{{v}_{0}^{2}+2gh}$=$\sqrt{25+2×10×7.2}$=13m/s
答:
(1)重力对小球所做的功为14.4J.
(2)小球落地时速度的大小v是13m/s.
点评 本题运用动能定理和机械能守恒两种方法研究斜抛运动,也可以采用运动的分解法求解v.但要注意体会功能关系应用的便捷.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
9. 如图所示,封闭着理想气体的气缸挂在弹簧下,弹簧秤的示数为F.已知气缸的质量为M,活塞质量为m,横截面积为S,活塞与缸体间摩擦不计,外界大气压强为P0,则缸内的压强为( )
如图所示,封闭着理想气体的气缸挂在弹簧下,弹簧秤的示数为F.已知气缸的质量为M,活塞质量为m,横截面积为S,活塞与缸体间摩擦不计,外界大气压强为P0,则缸内的压强为( )
 如图所示,封闭着理想气体的气缸挂在弹簧下,弹簧秤的示数为F.已知气缸的质量为M,活塞质量为m,横截面积为S,活塞与缸体间摩擦不计,外界大气压强为P0,则缸内的压强为( )
如图所示,封闭着理想气体的气缸挂在弹簧下,弹簧秤的示数为F.已知气缸的质量为M,活塞质量为m,横截面积为S,活塞与缸体间摩擦不计,外界大气压强为P0,则缸内的压强为( )| A. | P0-$\frac{mg}{s}$ | B. | P0-$\frac{Mg}{S}$ | C. | P0+$\frac{Mg-F}{S}$ | D. | P0+[$\frac{(M+m)g-F}{S}$] |
16. 如图所示,固定在水平地面上的物体A,左侧是圆弧面,右侧是倾角为θ的斜面,一根轻绳跨过物体A顶点上的小滑轮,绳两端分别系有质量为m1、m2的小球,当两球静止时,小球m1与圆心连线跟水平方向的夹角也为θ,不计一切摩擦,圆弧面半径远大于小球直径,则m1、m2之间的关系是( )
如图所示,固定在水平地面上的物体A,左侧是圆弧面,右侧是倾角为θ的斜面,一根轻绳跨过物体A顶点上的小滑轮,绳两端分别系有质量为m1、m2的小球,当两球静止时,小球m1与圆心连线跟水平方向的夹角也为θ,不计一切摩擦,圆弧面半径远大于小球直径,则m1、m2之间的关系是( )
 如图所示,固定在水平地面上的物体A,左侧是圆弧面,右侧是倾角为θ的斜面,一根轻绳跨过物体A顶点上的小滑轮,绳两端分别系有质量为m1、m2的小球,当两球静止时,小球m1与圆心连线跟水平方向的夹角也为θ,不计一切摩擦,圆弧面半径远大于小球直径,则m1、m2之间的关系是( )
如图所示,固定在水平地面上的物体A,左侧是圆弧面,右侧是倾角为θ的斜面,一根轻绳跨过物体A顶点上的小滑轮,绳两端分别系有质量为m1、m2的小球,当两球静止时,小球m1与圆心连线跟水平方向的夹角也为θ,不计一切摩擦,圆弧面半径远大于小球直径,则m1、m2之间的关系是( )| A. | m1=m2 | B. | m1=m2tanθ | C. | m1=m2cotθ | D. | m1=m2cosθ |
14. 如图所示,金属棒MN,在竖直放置的两根平行导轨上无摩擦地下滑,导轨间串联一个电阻,磁感强度垂直于导轨平面,金属棒和导轨的电阻不计,设MN下落过程中,电阻R上消耗的最大功率为P,要使R消耗的电功率增大到4P,可采取的方法是( )
如图所示,金属棒MN,在竖直放置的两根平行导轨上无摩擦地下滑,导轨间串联一个电阻,磁感强度垂直于导轨平面,金属棒和导轨的电阻不计,设MN下落过程中,电阻R上消耗的最大功率为P,要使R消耗的电功率增大到4P,可采取的方法是( )
 如图所示,金属棒MN,在竖直放置的两根平行导轨上无摩擦地下滑,导轨间串联一个电阻,磁感强度垂直于导轨平面,金属棒和导轨的电阻不计,设MN下落过程中,电阻R上消耗的最大功率为P,要使R消耗的电功率增大到4P,可采取的方法是( )
如图所示,金属棒MN,在竖直放置的两根平行导轨上无摩擦地下滑,导轨间串联一个电阻,磁感强度垂直于导轨平面,金属棒和导轨的电阻不计,设MN下落过程中,电阻R上消耗的最大功率为P,要使R消耗的电功率增大到4P,可采取的方法是( )| A. | 使MN的质量增大到原来的2倍 | |
| B. | 使磁感强度B增大到原来的2倍 | |
| C. | 使MN和导轨间距同时增大到原来的2倍 | |
| D. | 使电阻R的阻值减到原来的一半 |

 用如图所示的装置验证系统(滑块及重物)机械能守恒.滑块放在水平的气垫导轨上,滑块释放时遮光条与光电门间的距离为x(x<h).滑块质量M,重物质量m.
用如图所示的装置验证系统(滑块及重物)机械能守恒.滑块放在水平的气垫导轨上,滑块释放时遮光条与光电门间的距离为x(x<h).滑块质量M,重物质量m.
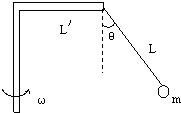 如图所示,已知绳长L=0.5m,水平杆L′=0.3m,小球质量m=0.3kg,整个装置可绕竖直轴匀速转动,问:(sin37°=0.6,cos37°=0.8,g=10m/s2,结果均保留三位有效数字)
如图所示,已知绳长L=0.5m,水平杆L′=0.3m,小球质量m=0.3kg,整个装置可绕竖直轴匀速转动,问:(sin37°=0.6,cos37°=0.8,g=10m/s2,结果均保留三位有效数字)