��Ŀ����
20��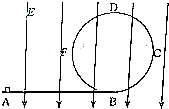 ��ͼ��ʾ��ABΪһ��Ե��ˮƽֱ�����BCDFΪһ��Ե�Ĺ⻬Բ�ι����BΪԲ�����͵㣬��ֱ��������ֱ�������ǿ�糡�У�BCDF�ǰ뾶ΪR��Բ�ι������������Ϊm�Ĵ������С���飨����Ϊ�ʵ㣩��һ���ٶ�v0��A�㿪ʼ�ع�������˶���С����ǡ��������ֱԲ�����������Բ���˶�����֪С������AB�����Ķ�Ħ������Ϊ�̣�A��B֮�����ΪL���糡ǿ��E=$\frac{mg}{q}$���������ٶ�Ϊg����
��ͼ��ʾ��ABΪһ��Ե��ˮƽֱ�����BCDFΪһ��Ե�Ĺ⻬Բ�ι����BΪԲ�����͵㣬��ֱ��������ֱ�������ǿ�糡�У�BCDF�ǰ뾶ΪR��Բ�ι������������Ϊm�Ĵ������С���飨����Ϊ�ʵ㣩��һ���ٶ�v0��A�㿪ʼ�ع�������˶���С����ǡ��������ֱԲ�����������Բ���˶�����֪С������AB�����Ķ�Ħ������Ϊ�̣�A��B֮�����ΪL���糡ǿ��E=$\frac{mg}{q}$���������ٶ�Ϊg������1��С������AB��������ܵĻ���Ħ�����Ĵ�С��
��2��ǡ����Բ���������ߵ�Dʱ���ٶ�vD�Ĵ�С��
��3��С����ij��ٶ�v0�Ĵ�С��
���� ��1���ɻ�������������������AB�����ѹ��������f=��N��Ħ������
��2��С����ǡ��������ֱԲ�����������Բ���˶�����D�㣬�������͵糡���ĺ����ṩ����������ţ�ٵڶ�������vD��
��3�����������̣����ö��ܶ�����ʽ�����ٶ�v0�Ĵ�С��
��� �⣺��1���������ܵĵ糡����С F=qE=mg��������ֱ���£���С������AB��������ܵĻ���Ħ�����Ĵ�С f=�̣�mg+F��=2��mg��
��2����D�㣬��ţ�ٵڶ����ɵ�
F+mg=m$\frac{{v}_{D}^{2}}{R}$
��� vD=$\sqrt{2gR}$
��3�����������̣��ɶ��ܶ�����
-fL-��F+mg��•2R=$\frac{1}{2}m{v}_{D}^{2}$-$\frac{1}{2}m{v}_{0}^{2}$
��� v0=$\sqrt{10gR+4��gL}$
��
��1��С������AB��������ܵĻ���Ħ�����Ĵ�СΪ2��mg��
��2��ǡ����Բ���������ߵ�Dʱ���ٶ�vD�Ĵ�СΪ$\sqrt{2gR}$��
��3��С����ij��ٶ�v0�Ĵ�СΪ$\sqrt{10gR+4��gL}$��
���� �ڱ��������岻�������������ã����е糡�����ڽ���Ĺ����У�һ��Ҫ�������������������˶����̣��ر���С��ǡ�ù�D������������ݶ��ܶ�����ţ�ٵڶ����������ʽ��⣮

| A�� | ��0��1s�ڣ����������� | B�� | ��0��2s�ڣ��������������� | ||
| C�� | ��1s��2s�ڣ����������� | D�� | ��0��3s�ڣ��������������� |
| A�� | ���ٶ� | B�� | ���ٶ� | C�� | ���ļ��ٶ� | D�� | ת�� |
| A�� | 1275m | B�� | 800m | C�� | 1445m | D�� | 500m |
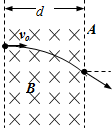 ��ͼ��ʾ��һ���������ٶ�v0��ֱ����Ÿ�Ӧǿ��ΪB����Ϊd����ǿ�ų��У������ų����ٶȷ��������ԭ�������䷽��ļн�Ϊ30�㣬�������������Բ��ƣ���
��ͼ��ʾ��һ���������ٶ�v0��ֱ����Ÿ�Ӧǿ��ΪB����Ϊd����ǿ�ų��У������ų����ٶȷ��������ԭ�������䷽��ļн�Ϊ30�㣬�������������Բ��ƣ��� ��ͼ��ʾ��A��BΪ������е������ֵ�ɵ�ƽ�н����壬�������10cm�������ĵ��Ʋ�Ϊ40V��M��NΪ�������㣬M����A�塢N����B��ľ��붼��3cm����
��ͼ��ʾ��A��BΪ������е������ֵ�ɵ�ƽ�н����壬�������10cm�������ĵ��Ʋ�Ϊ40V��M��NΪ�������㣬M����A�塢N����B��ľ��붼��3cm���� Ϊ�����ú�����Դ������������ʱ����ˮ���и�شų��������ĸ� Ӧ�綯����������ˮ�����٣����躣��ij���ĵشų���ֱ����ΪB=0.5��10-4T��ˮ�����ϱ�������ͼ�������缫��ֱ����˴���ˮ�У��ұ������缫�����ߴ�ֱˮ���������������L=10m�������缫������������ѹ���Ķ���ΪU=2mV����ˮ�����ٴ�СΪ4m/s��
Ϊ�����ú�����Դ������������ʱ����ˮ���и�شų��������ĸ� Ӧ�綯����������ˮ�����٣����躣��ij���ĵشų���ֱ����ΪB=0.5��10-4T��ˮ�����ϱ�������ͼ�������缫��ֱ����˴���ˮ�У��ұ������缫�����ߴ�ֱˮ���������������L=10m�������缫������������ѹ���Ķ���ΪU=2mV����ˮ�����ٴ�СΪ4m/s��