题目内容
9. 如图所示,质量为m=1kg、电荷量为q=5×10-2C的带正电的小滑块,从半径为R=0.4m的光滑绝缘$\frac{1}{4}$圆弧轨道上由静止自A端滑下.整个装置处在方向互相垂直的匀强电场与匀强磁场中.已知E=100V/m,方向水平向右,B=1T,方向垂直纸面向里,g=10m/s2.求:
如图所示,质量为m=1kg、电荷量为q=5×10-2C的带正电的小滑块,从半径为R=0.4m的光滑绝缘$\frac{1}{4}$圆弧轨道上由静止自A端滑下.整个装置处在方向互相垂直的匀强电场与匀强磁场中.已知E=100V/m,方向水平向右,B=1T,方向垂直纸面向里,g=10m/s2.求:(1)滑块到达C点时的速度;
(2)在C点时滑块所受洛伦兹力.
分析 (1)分析滑块受力情况,根据动能定理可求得滑块到达C点的速度;
(2)根据洛伦兹力公式可求得滑块所受洛伦兹力.
解答 解:(1)以滑块为研究对象,自轨道上A点滑到C点的过程中,受重力mg,方向竖直向下;静电力qE,方向水平向右;
洛伦兹力F洛=qvB,方向始终垂直于速度方向.滑块从A到C过程中洛伦兹力不做功,由动能定理得:
mgR-qER=$\frac{1}{2}m{v}_{0}^{2}$
得:vC=$\sqrt{\frac{2(mg-qE)R}{m}}$=$\sqrt{\frac{2×1×10×0.4-2×5×1{0}^{-2}×100}{1}}$=2 m/s.方向水平向左.
(2)根据洛伦兹力公式得:F=qvCB=5×10-2×2×1 N=0.1 N,方向竖直向下.
答:(1)滑块到达C点时的速度为2m/s;方向水平向左;
(2)在C点时滑块所受洛伦兹力为2m/s.
点评 本题考查带电粒子的运动,要注意明确动能定理的应用,知道洛伦兹力永不做功这一重要特点.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
17.关于热现象,下列说法正确的是( )
| A. | 物体的动能和重力势能也是其内能的一部分 | |
| B. | 悬浮在液体中的颗粒越小,温度越高,布朗运动越剧烈 | |
| C. | 液晶与多晶体一样具有各向同性 | |
| D. | 当分子间的引力与斥力平衡时,分子势能最小 | |
| E. | 若一定质量的理想气体在膨胀的同时放出热量,则气体分子的平均动能减小 |
4.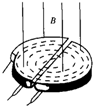 回旋加速器是获得高能带电粒子的装置,其核心部分是分别与高频交流电源的两极相连的两个D形盒,两盒间的狭缝中形成周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示,关于回旋加速器的下列说法正确的是( )
回旋加速器是获得高能带电粒子的装置,其核心部分是分别与高频交流电源的两极相连的两个D形盒,两盒间的狭缝中形成周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示,关于回旋加速器的下列说法正确的是( )
 回旋加速器是获得高能带电粒子的装置,其核心部分是分别与高频交流电源的两极相连的两个D形盒,两盒间的狭缝中形成周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示,关于回旋加速器的下列说法正确的是( )
回旋加速器是获得高能带电粒子的装置,其核心部分是分别与高频交流电源的两极相连的两个D形盒,两盒间的狭缝中形成周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示,关于回旋加速器的下列说法正确的是( )| A. | 带电粒子从D形盒射出时的动能与加速电压无关 | |
| B. | 带电粒子从D形盒射出时的动能与磁场的强弱有关 | |
| C. | 带电粒子做一次圆周运动,要被加速两次,因此交变电场的周期应为圆周运动周期的二倍 | |
| D. | 用同一回旋加速器分别加速不同的带电粒子,不用调节交变电场的频率 |
14.某人用手将10kg的物体由静止竖直向上提起1m,此时物体的速度为2m/s(g取10m/s2),则下列说法正确的是( )
| A. | 手对物体做功120J | B. | 手对物体做功20J | ||
| C. | 重力做功100J | D. | 物体重力势能增加100J |
1.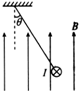 一长L=0.5m、质量m=0.2kg的水平直导线通过绝缘细线悬挂在天花板上,整个装置处于方向竖直向上的匀强磁场B中.当导线中通以垂直于纸面向里大小为I=10A的电流,该导线静止时细线与竖直方向间的夹角θ=37°,如图所示.现保持磁感应强度的大小不变,让磁场方向在纸面内沿逆时针方向缓慢转过90°,取重力加速度g=10m/s2,已知sin37°=0.6,则下列说法中正确的有( )
一长L=0.5m、质量m=0.2kg的水平直导线通过绝缘细线悬挂在天花板上,整个装置处于方向竖直向上的匀强磁场B中.当导线中通以垂直于纸面向里大小为I=10A的电流,该导线静止时细线与竖直方向间的夹角θ=37°,如图所示.现保持磁感应强度的大小不变,让磁场方向在纸面内沿逆时针方向缓慢转过90°,取重力加速度g=10m/s2,已知sin37°=0.6,则下列说法中正确的有( )
 一长L=0.5m、质量m=0.2kg的水平直导线通过绝缘细线悬挂在天花板上,整个装置处于方向竖直向上的匀强磁场B中.当导线中通以垂直于纸面向里大小为I=10A的电流,该导线静止时细线与竖直方向间的夹角θ=37°,如图所示.现保持磁感应强度的大小不变,让磁场方向在纸面内沿逆时针方向缓慢转过90°,取重力加速度g=10m/s2,已知sin37°=0.6,则下列说法中正确的有( )
一长L=0.5m、质量m=0.2kg的水平直导线通过绝缘细线悬挂在天花板上,整个装置处于方向竖直向上的匀强磁场B中.当导线中通以垂直于纸面向里大小为I=10A的电流,该导线静止时细线与竖直方向间的夹角θ=37°,如图所示.现保持磁感应强度的大小不变,让磁场方向在纸面内沿逆时针方向缓慢转过90°,取重力加速度g=10m/s2,已知sin37°=0.6,则下列说法中正确的有( )| A. | 磁场未转动时,绝缘细线对通电导线的拉力大小为2.5N | |
| B. | 该磁场的磁感应强度大小为1.5T | |
| C. | 转动过程中绝缘细线与竖直方向的夹角先变大后变小 | |
| D. | 转动过程中绝缘细线受到的拉力最小值为1.6N |
18.弹簧振子做机械振动,若从平衡位置O开始计时,经过0.3s时,振子第一次经过P点,又经过了0.2s,振子第二次经过P点,则该振子第三次经过P点是所需的时间为( )
| A. | 1.6s | B. | 1.1s | C. | 0.8s | D. | 0.33s |
