题目内容
1．物体从某一初速度冲上倾角为30°的斜面，经2s沿斜面上升12m后又开始下滑，求物体从最高点返回原处的时间．分析 由经2s沿斜面上升12m后又开始下滑，结合受力分析和牛顿第二定律可得摩擦因数，由受力分析和牛顿第二定律可得返回时的加速度大小，由位移时间关系可得时间
解答 解：由题意知，上升阶段的合力为：F=mgsin30°+μmgcos30°…①
上升阶段的加速度为：a=$\frac{F}{m}$…②
采用逆向思维法，由运动学公式得，$\frac{1}{2}$at2=x…③
联立①②③得，μ=0.125…④
返回阶段，加速大小为：a′=gsin30°-μgcos30°…⑤
返回过程有：x=$\frac{1}{2}$at′2…⑥
联立④⑤⑥可得：t′=2.45s
答：物体从最高点返回原处的时间约为2.45s
点评 本题关键根据受力情况确定加速度，然后根据运动学公式确定运动学参量，对于匀减速到停止的情况，大胆的采用逆向思维法是很好的．
练习册系列答案
一线名师提优试卷系列答案
相关题目
11．在探究“加速度与质量、合外力关系”的实验中，使用了电磁式打点计时器，若该打点计时器使用的是电压为6V的交流电源，则以下说法正确的是（ ）
| A． | 该电源电压的最大值为6V | B． | 该电源电压的有效值为6V | ||
| C． | 该电源电压的最大值为12V |
9．若以M表示水的摩尔质量，V表示在标准状态下水蒸气的摩尔体积，ρ为在标准状态下水蒸气的密度，NA为阿伏加德罗常数，m、V0表示每个水分子的质量和体积．下面关系式正确的是（ ）
| A． | NA=$\frac{Vρ}{m}$ | B． | ρ=$\frac{M}{{N}_{A}{V}_{0}}$ | C． | m=$\frac{M}{{N}_{A}}$ | D． | V0=$\frac{V}{{N}_{A}}$ |
如图，质量为M的导热性能极好的气缸，高为L，开口向上置于水平地面上，气缸中有横截面积为S、质量为m的光滑活塞，活塞将一定质量的理想气体封闭在气缸内．外界温度为t1、大气压为p0，此时气柱高度为l，气缸和活塞的厚度均可忽略不计，重力加速度为g．
如图所示，BC为半径等于$\frac{2}{5}$$\sqrt{2}$m竖直放置的光滑细圆管，O为细圆管的圆心，在圆管的末端C连接倾斜角为45°、动摩擦因数μ=0.6的足够长粗糙斜面，一小球从O点正上方某处A点以v0水平抛出，恰好能垂直OB从B点进入细圆管．（g=10m/s2），小球从O点的正上方某处A点水平抛出的初速度v0为多少？
1．
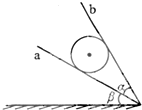如图所示，质量为m的钢球静止于两光滑木板a、b之间，已知两木板的夹角α=30°，a木板与水平面的夹角β=30°，则钢球对a、b板的压力大小Fa、Fb分别是（ ）
如图所示，质量为m的钢球静止于两光滑木板a、b之间，已知两木板的夹角α=30°，a木板与水平面的夹角β=30°，则钢球对a、b板的压力大小Fa、Fb分别是（ ）| A． | Fa=mg，Fb=mg | B． | Fa=$\sqrt{3}$mg，Fb=$\frac{\sqrt{3}}{2}$mg | C． | Fa=$\frac{\sqrt{3}}{2}$mg，Fb=$\sqrt{3}$mg | D． | Fa=$\sqrt{3}$mg，Fb=mg |
18．下列说法正确的是（ ）
| A． | ${\;}_{7}^{15}$N+${\;}_{1}^{1}$H→${\;}_{6}^{12}$C+${\;}_{2}^{4}$He是α衰变方程 | |
| B． | ${\;}_{1}^{1}$H+${\;}_{1}^{2}$H→${\;}_{2}^{3}$He+γ是核聚变反应方程 | |
| C． | ${\;}_{92}^{238}$U→${\;}_{90}^{234}$Th+${\;}_{2}^{4}$He是核裂变反应方程 | |
| D． | ${\;}_{2}^{4}$He+${\;}_{13}^{27}$Al→${\;}_{15}^{30}$P+${\;}_{0}^{1}$n是原子核的人工转变方程 |
