题目内容
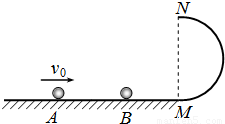
在光滑的水平面上,一质量为mA=0.1kg的小球A,以8m/s的初速度向右运动,与质量为mB=0.2kg的静止小球B发生弹性正碰.碰后小球B滑向与水平面相切、半径为R=0.5m的竖直放置的光滑半圆形轨道,且恰好能通过最高点N后水平抛出.g=10m/s2.求:(1)碰撞后小球B的速度大小;(2)小球B从轨道最低点M运动到最高点N的过程中所受合外力的冲量;
(3)碰撞过程中系统的机械能损失.
【答案】分析:(1)小球恰好能通过最高点N,说明小球到达最高点时小球的重力提供向心力,由牛顿第二定律求出小球到达N点的速度,由动能定理可以求出碰撞后小球B的速度.
(2)由动量定理可以求出合外力的冲量.
(3)由能量守恒定律可以求出碰撞过程中机械能的损失.
解答:解:(1)小球B在最高点N时,由牛顿第二定律得:
mBg=mB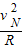 ,解得:vN=
,解得:vN=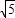 m/s;
m/s;
小球从最低点运动到最高点的过程中,
由动能定理得:-2mBgR= mBvN2-
mBvN2- mBvM2,
mBvM2,
解得:vM=5m/s;
(2)以向右为正方向,从M到N过程,
由动量定理得:I=mBvN-mBvM=-(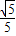 +1)N?s,方向向左;
+1)N?s,方向向左;
(3)碰撞过程动量守恒,由动量守恒定律得:
mAv=mAvA+mBvB,vB=vM,解得:vA=-2m/s;
碰撞过程中,由能量守恒定律可得:
损失的机械能为△E= mAv2-
mAv2- mAvA2-
mAvA2- mBvB2=0.5J;
mBvB2=0.5J;
答:(1)碰撞后小球B的速度大小为5m/s;
(2)小球B从轨道最低点M运动到最高点N的过程中所受合外力的冲量大小为(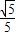 +1)N?s,方向向左;
+1)N?s,方向向左;
(3)碰撞过程中系统的机械能损失为0.5J.
点评:熟练应用牛顿第二定律、动能定理、能量守恒定律即可正确解题.
(2)由动量定理可以求出合外力的冲量.
(3)由能量守恒定律可以求出碰撞过程中机械能的损失.
解答:解:(1)小球B在最高点N时,由牛顿第二定律得:
mBg=mB
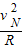 ,解得:vN=
,解得:vN=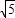 m/s;
m/s;小球从最低点运动到最高点的过程中,
由动能定理得:-2mBgR=
 mBvN2-
mBvN2- mBvM2,
mBvM2,解得:vM=5m/s;
(2)以向右为正方向,从M到N过程,
由动量定理得:I=mBvN-mBvM=-(
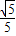 +1)N?s,方向向左;
+1)N?s,方向向左;(3)碰撞过程动量守恒,由动量守恒定律得:
mAv=mAvA+mBvB,vB=vM,解得:vA=-2m/s;
碰撞过程中,由能量守恒定律可得:
损失的机械能为△E=
 mAv2-
mAv2- mAvA2-
mAvA2- mBvB2=0.5J;
mBvB2=0.5J;答:(1)碰撞后小球B的速度大小为5m/s;
(2)小球B从轨道最低点M运动到最高点N的过程中所受合外力的冲量大小为(
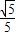 +1)N?s,方向向左;
+1)N?s,方向向左;(3)碰撞过程中系统的机械能损失为0.5J.
点评:熟练应用牛顿第二定律、动能定理、能量守恒定律即可正确解题.

练习册系列答案
相关题目
 在光滑的水平面上有一直角坐标系,现有一个质量m=0.1kg的小球,从y轴正半轴上的P1点以速度v0=0.6m/s垂直于y轴射入.已知小球在y>0的空间内受到一个恒力F1的作用,方向沿y轴负方向,在y<0的空间内小球受到一平行于水平面、大小不变F2的作用,且F2的方向与小球的速度方向始终垂直.现小球从P1点进入坐标系后,经x=1.2m的P2点与x轴正方向成53°角射入y<0的空间,最后从y轴负半轴上的P3点垂直于y轴射出.如图所示,(已知:sin53°=0.8,cos53°=0.6).求:
在光滑的水平面上有一直角坐标系,现有一个质量m=0.1kg的小球,从y轴正半轴上的P1点以速度v0=0.6m/s垂直于y轴射入.已知小球在y>0的空间内受到一个恒力F1的作用,方向沿y轴负方向,在y<0的空间内小球受到一平行于水平面、大小不变F2的作用,且F2的方向与小球的速度方向始终垂直.现小球从P1点进入坐标系后,经x=1.2m的P2点与x轴正方向成53°角射入y<0的空间,最后从y轴负半轴上的P3点垂直于y轴射出.如图所示,(已知:sin53°=0.8,cos53°=0.6).求: 如图所示,在光滑的水平面上,一根水平细线两端分别连接A、B两个物体,已知A、B质量分别为m1=2kg,m2=1kg,细线能承受的最大拉力是10N.要使系统的加速度最大,应
如图所示,在光滑的水平面上,一根水平细线两端分别连接A、B两个物体,已知A、B质量分别为m1=2kg,m2=1kg,细线能承受的最大拉力是10N.要使系统的加速度最大,应 (2009?湘潭模拟)在光滑的水平面上有一质量M=2kg的木板A,其右端挡板上固定一根轻质弹簧,在靠近木板左端的P处有一大小忽略不计质量m=2kg的滑块B.木板上Q处的左侧粗糙,右侧光滑.且PQ间距离L=2m,如图所示.某时刻木板A以υA=1m/s的速度向左滑行,同时滑块B以υB=5m/s的速度向右滑行,当滑块B与P处相距
(2009?湘潭模拟)在光滑的水平面上有一质量M=2kg的木板A,其右端挡板上固定一根轻质弹簧,在靠近木板左端的P处有一大小忽略不计质量m=2kg的滑块B.木板上Q处的左侧粗糙,右侧光滑.且PQ间距离L=2m,如图所示.某时刻木板A以υA=1m/s的速度向左滑行,同时滑块B以υB=5m/s的速度向右滑行,当滑块B与P处相距 (2013?淮安模拟)如图所示,在光滑的水平面上有一质量为M、倾角为θ的光滑斜面,一质量为m的物块从斜面上由静止下滑.下面给出的物块在下滑过程中对斜面压力大小FN的四个表达式中,只有一个是正确的,你可能不会求解,但是你可以通过分析,对下列表达式做出合理的判断.根据你的判断,合理的表达式应为( )
(2013?淮安模拟)如图所示,在光滑的水平面上有一质量为M、倾角为θ的光滑斜面,一质量为m的物块从斜面上由静止下滑.下面给出的物块在下滑过程中对斜面压力大小FN的四个表达式中,只有一个是正确的,你可能不会求解,但是你可以通过分析,对下列表达式做出合理的判断.根据你的判断,合理的表达式应为( )