题目内容
如图所示,在边长为a的正方形区域内有匀强磁场,磁感应强度为B,其方向垂直纸面向外,一个边长也为a的单匝正方形导线框架EFGH正好与上述磁场区域的边界重合,导线框的电阻为R.现使导线框以周期T绕其中心O点在纸面内匀速转动,经过八分之一T 导线框转到图中虚线位置,则在这八分之一T 时间内( )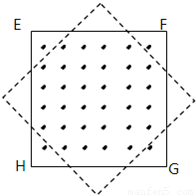
A.顺时针方向转动时,感应电流方向为E→F→G→H→E
B.平均感应电动势大小等于
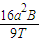
C.平均感应电动势大小等于
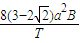
D.通过导线框横截面的电荷量为
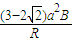
【答案】分析:根据楞次定律判断感应电流的方向.
运用法拉第电磁感应定律求出平均感应电动势大小.
根据电量的表达式求出通过导线框横截面的电荷量.
解答:解:A、由于虚线位置是经过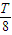 到达的,而且线框是顺时针方向转动,所以线框的磁通量是变小的.
到达的,而且线框是顺时针方向转动,所以线框的磁通量是变小的.
根据楞次定律,感应电流产生的磁场跟原磁场方向相同,即感应电流产生的磁场方向为垂直纸面向外,根据右手定则,我们可以判断出感应电流的方向为:E→H→G→F→E,故A错误.
B、根据法拉第电磁感应定律得:平均感应电动势E=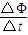 =
=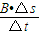
根据几何关系找出有磁场穿过面积的变化△s=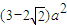
解得:E=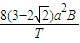 ,故B错误.
,故B错误.
C、通过B选项分析知道平均感应电动势,故C正确.
D、通过导线框横截面的电荷量q=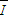 t=
t=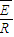 t=
t=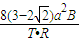 ?
?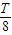 =
=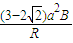 ,故D正确.
,故D正确.
故选CD.
点评:对于感应电流方向的判断要按照步骤解决.
结合几何关系能够找出有效面积的变化.
运用法拉第电磁感应定律求出平均感应电动势大小.
根据电量的表达式求出通过导线框横截面的电荷量.
解答:解:A、由于虚线位置是经过
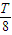 到达的,而且线框是顺时针方向转动,所以线框的磁通量是变小的.
到达的,而且线框是顺时针方向转动,所以线框的磁通量是变小的.根据楞次定律,感应电流产生的磁场跟原磁场方向相同,即感应电流产生的磁场方向为垂直纸面向外,根据右手定则,我们可以判断出感应电流的方向为:E→H→G→F→E,故A错误.
B、根据法拉第电磁感应定律得:平均感应电动势E=
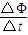 =
=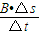
根据几何关系找出有磁场穿过面积的变化△s=
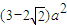
解得:E=
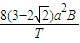 ,故B错误.
,故B错误.C、通过B选项分析知道平均感应电动势,故C正确.
D、通过导线框横截面的电荷量q=
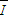 t=
t=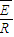 t=
t=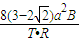 ?
?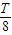 =
=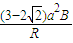 ,故D正确.
,故D正确.故选CD.
点评:对于感应电流方向的判断要按照步骤解决.
结合几何关系能够找出有效面积的变化.

练习册系列答案
相关题目
 如图所示,在边长为a的等边三角形区域内有匀强磁场B,其方向垂直纸面向外,一个边长也为a的等边三角形导体框EFG正好与上述磁场区域重合,之后以周期T绕其几何中心O点在纸面内匀速转动,于是框架EFG中产生感应电动势,经
如图所示,在边长为a的等边三角形区域内有匀强磁场B,其方向垂直纸面向外,一个边长也为a的等边三角形导体框EFG正好与上述磁场区域重合,之后以周期T绕其几何中心O点在纸面内匀速转动,于是框架EFG中产生感应电动势,经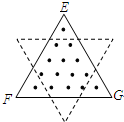 (2013?虹口区二模)如图所示,在边长为a的等边三角形区域内有匀强磁场B,其方向垂直纸面向外,一个边长也为a的等边三角形导线框架EFG正好与上述磁场区域的边界重合,现使导线框以周期T绕其中心O点在纸面内匀速转动,经过
(2013?虹口区二模)如图所示,在边长为a的等边三角形区域内有匀强磁场B,其方向垂直纸面向外,一个边长也为a的等边三角形导线框架EFG正好与上述磁场区域的边界重合,现使导线框以周期T绕其中心O点在纸面内匀速转动,经过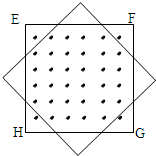 如图所示,在边长为a的正方形区域内有匀强磁场,磁感应强度为B,其方向垂直纸面向外,一个边长也为a的正方形形导线框架EFGH正好与上述磁场区域的边界重合,现使导线框以周期T绕其中心O点在纸面内匀速转动,经过
如图所示,在边长为a的正方形区域内有匀强磁场,磁感应强度为B,其方向垂直纸面向外,一个边长也为a的正方形形导线框架EFGH正好与上述磁场区域的边界重合,现使导线框以周期T绕其中心O点在纸面内匀速转动,经过 (2004?南京三模)如图所示,在边长为a的等边三角形bcd所围区域内有磁感应强度大小为B、方向垂直纸面向内的匀强磁场,某时刻静止于b点处的原子核X发生α衰变.α粒子沿bc方向射入磁场,经磁场偏转后恰好由d点射出且与cd边相切.已知α粒子质量为m、电荷量为2e,剩余核的质量为M,衰变过程释放的核能全部转化为动能,求
(2004?南京三模)如图所示,在边长为a的等边三角形bcd所围区域内有磁感应强度大小为B、方向垂直纸面向内的匀强磁场,某时刻静止于b点处的原子核X发生α衰变.α粒子沿bc方向射入磁场,经磁场偏转后恰好由d点射出且与cd边相切.已知α粒子质量为m、电荷量为2e,剩余核的质量为M,衰变过程释放的核能全部转化为动能,求 如图所示,在边长为a的等边三角形区域内有匀强磁场B,其方向垂直纸面向外.一个边长也为a的等边三角形导线框架EFG正好与上述磁场区域的边界重合.现使导线框以周期T绕其中心O点在纸面内匀速转动,经过
如图所示,在边长为a的等边三角形区域内有匀强磁场B,其方向垂直纸面向外.一个边长也为a的等边三角形导线框架EFG正好与上述磁场区域的边界重合.现使导线框以周期T绕其中心O点在纸面内匀速转动,经过