题目内容
如图3所示,在直角坐标系的第一、二象限内有垂直于纸面的匀强磁场,第三象限有沿Y轴负方向的匀强电场,第四象限内无电场和磁场。质量为m、带电量为q的粒子从M点以速度v0沿x轴负方向进入电场,不计粒子的重力,粒子经N、P最后又回到M点。设OM=L,ON=2L,则:
关于电场强度E的大小,下列结论正确的是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(2)匀强磁场的方向是 。
(3)磁感应强度B的大小是多少?


(1)C。(2)由左手定则,匀强磁场的方向为垂直纸面向里。(3)![]()
解析:
(1)由带电粒子在电场中做类平抛运动,易知![]() ,且
,且![]() 则E=
则E=![]() 故选C
故选C
(2)由左手定则,匀强磁场的方向为垂直纸面向里。
(3)根据粒子在电场中运动的情况可知,粒子带负电。粒子在电场中做类平抛运动,设到达N点的速度为v,运动方向与x轴负方向的夹角为θ,如图4所示。
由动能定理得![]()
将(1)式中的E代入可得![]() 所以θ=45°
所以θ=45°
粒子在磁场中做匀速圆周运动,经过P点时速度方向也与x轴负方向成45°角。
则OP=OM=L NP=NO+OP=3L
粒子在磁场中的轨道半径为R=Npcos45°=![]() 又
又![]()
解得 ![]()

练习册系列答案
相关题目
 (2006?盐城模拟)如图所示,在直角坐系中的第Ⅰ象限中存在沿y轴负方向的匀强电场,在第Ⅳ象限中存在垂直纸面的匀强磁场,一质量为m、带电量为q的粒子(不计重力)在y轴上的A(0,3)以平行x轴的初速度v0=120m/s射人电场区,然后从电场区进入磁场区,又从磁场区进入电场区,并通过x轴上P点(4.5,0)和Q点(8,0)各一次.已知该粒子的荷质比为
(2006?盐城模拟)如图所示,在直角坐系中的第Ⅰ象限中存在沿y轴负方向的匀强电场,在第Ⅳ象限中存在垂直纸面的匀强磁场,一质量为m、带电量为q的粒子(不计重力)在y轴上的A(0,3)以平行x轴的初速度v0=120m/s射人电场区,然后从电场区进入磁场区,又从磁场区进入电场区,并通过x轴上P点(4.5,0)和Q点(8,0)各一次.已知该粒子的荷质比为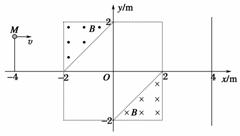


 =108C/kg,求磁感应强度的大小与方向?
=108C/kg,求磁感应强度的大小与方向?