题目内容
18.一平板车静放在光滑水平地面上,其右端放一质量m=5kg的物体.平板车质量M=10kg,总长度L=1.5m,上表面离地高度h=1.25m,与物体间的动摩擦因数μ=0.2,物体可看成质点,所受的最大静摩擦力与滑动摩擦力相等,空气阻力可忽略,重力加速度g=10m/s2,现在平板车上施加一水平向右F=60N的拉力,求: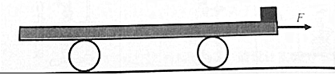
(1)物体刚脱离小车时的速度;
(2)当物体落地时,距离平板车左端的水平距离.
分析 (1)隔离对物体和平板车分析,根据牛顿第二定律求出加速度的大小,结合位移之差等于L求出运动的时间,根据速度时间公式求出物体刚脱离小车时的速度;
(2)根据高度求出平抛运动的时间,结合牛顿第二定律求出物体离开平板车后的加速度大小,结合物块的速度求出水平位移,根据平板车的速度和加速度求出匀加速直线运动的位移,通过位移之差求出当物体落地时距离平板车左端的水平距离.
解答 解:(1)隔离对物体分析,物体的加速度大小为:
${a}_{1}=\frac{μmg}{m}=μg=0.2×10m/{s}^{2}$=2m/s2.
小车的加速度为:
${a}_{2}=\frac{F-μmg}{M}=\frac{60-0.2×50}{10}=5m/{s}^{2}$,
根据$\frac{1}{2}{a}_{2}{t}^{2}-\frac{1}{2}{a}_{1}{t}^{2}=L$得代入数据解得:t=1s,
则物体刚脱离小车时的速度为:
v1=a1t=2×1m/s=2m/s.
(2)根据h=$\frac{1}{2}gt{′}^{2}$得物体离开平板车做平抛运动的时间为:
$t′=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2×1.25}{10}}s=0.5s$.
物体平抛运动的水平位移为:
x1=v1t′=2×0.5m=1m,
物体离开平板车后,平板车的加速度为:
${a}_{3}=\frac{F}{M}=\frac{60}{10}m/{s}^{2}=6m/{s}^{2}$,
物体离开平板车时,平板车的速度为:
v2=a2t=5×1m/s=5m/s,
则平板车的位移为:
${x}_{2}={v}_{2}t′+\frac{1}{2}{a}_{3}t{′}^{2}$=$5×0.5+\frac{1}{2}×6×0.25m$=3.25m,
当物体落地时,距离平板车左端的水平距离为:
△x=x2-x1=3.25-1m=2.25m.
答:(1)物体刚脱离小车时的速度为2m/s;
(2)当物体落地时,距离平板车左端的水平距离为2.25m.
点评 解决本题的关键理清物体和平板车在整个过程中的运动规律,结合牛顿第二定律和运动学公式综合求解,知道加速度是联系力学和运动学的桥梁.

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案| A. |  | B. |  | C. |  | D. |  |
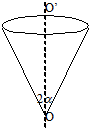 如图,一内壁光滑的圆锥面,顶点O在下方,锥角为2α,OO′是竖直轴线,若有两个相同的小珠(均视为质点)在圆锥的内壁上沿不同的圆轨道运动,则( )
如图,一内壁光滑的圆锥面,顶点O在下方,锥角为2α,OO′是竖直轴线,若有两个相同的小珠(均视为质点)在圆锥的内壁上沿不同的圆轨道运动,则( )| A. | 它们的向心力之比等于半径之比 | |
| B. | 它们的周期之比等于半径之比 | |
| C. | 它们的动能之比等于半径之比 | |
| D. | 设O点为势能零点,它们的动能之比等于重力势能之比 |
 如图所示,置于地面的矩形框架中用两细绳拴住质量为m的小球,绳B水平.设绳A、B对球的拉力大小分别为F1、F2,它们的合力大小为F.现将框架在竖直平面内绕左下端缓慢旋转90°,在此过程中( )
如图所示,置于地面的矩形框架中用两细绳拴住质量为m的小球,绳B水平.设绳A、B对球的拉力大小分别为F1、F2,它们的合力大小为F.现将框架在竖直平面内绕左下端缓慢旋转90°,在此过程中( )| A. | F1先增大后减小 | B. | F2先增大后减小 | C. | F先增大后减小 | D. | F先减小后增大 |
| A. | 电子的衍射图样表明电子具有波动性 | |
| B. | 太阳辐射的能量主要来自太阳内部的热核反应 | |
| C. | 氢原子从某激发态跃迁至基态要吸收特定频率的光子 | |
| D. | 结合能越大,原子核中核子结合得越牢固,原子核越稳定 |
 如图,竖直平面内有一半径为1.6m、长为10cm的光滑圆弧轨道,小球置于圆弧左端,t=0时刻起由静止释放.取g=10m/s2,t=2s时小球正在( )
如图,竖直平面内有一半径为1.6m、长为10cm的光滑圆弧轨道,小球置于圆弧左端,t=0时刻起由静止释放.取g=10m/s2,t=2s时小球正在( )| A. | 向右加速运动 | B. | 向右减速运动 | C. | 向左加速运动 | D. | 向左减速运动 |
 如图所示为龙门吊车的示意图,龙门架A、B的宽度L=10m,天车通过钢缆吊运货物入车以速度v在水平横梁上向右匀速移动,同时货物以a=2.5m/s2的加速度开始匀速上升,钢缆足够长.在天车从A到B的过程中,下列说法正确的是( )
如图所示为龙门吊车的示意图,龙门架A、B的宽度L=10m,天车通过钢缆吊运货物入车以速度v在水平横梁上向右匀速移动,同时货物以a=2.5m/s2的加速度开始匀速上升,钢缆足够长.在天车从A到B的过程中,下列说法正确的是( )| A. | 天车的速度v越大,货物的末速度越大 | |
| B. | 天车的速度v越大,货物的末速度越小 | |
| C. | 天车的速度v越大,货物的末速度不变 | |
| D. | 天车的速度v取某一数值时,货物的末速度有一最小值 |
 带电油滴以水平速度v0垂直进入磁场,并恰好做匀速度直线运动,如图所示,若油滴的质量为m,磁感应强度大小为B,则下列说法正确的是( )
带电油滴以水平速度v0垂直进入磁场,并恰好做匀速度直线运动,如图所示,若油滴的质量为m,磁感应强度大小为B,则下列说法正确的是( )| A. | 油滴必带正电荷,电荷量为$\frac{mg}{{v}_{0}B}$ | |
| B. | 油滴必带正电荷,电荷量为$\frac{2mg}{{v}_{0}B}$ | |
| C. | 油滴必带负电荷,比何$\frac{q}{m}$=$\frac{g}{{v}_{0}B}$ | |
| D. | 油滴带什么电荷都可以,只要满足q=$\frac{mg}{{v}_{0}B}$ |