题目内容
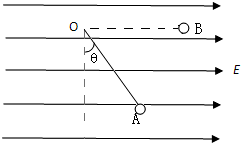 如图所示,在方向水平向右的匀强电场中,一长为L的不可伸长的不导电细线的一端连着一个质量为m的带电量为q小球,另一端固定于O点,小球恰能静止于电场中A点,OA连线与竖直向成θ角且θ=37°.现把小球拉起至细线成水平方向(如图中虚线OB所示),然后无初速释放.(取sin37°=0.6,cos37°=0.8)求:
如图所示,在方向水平向右的匀强电场中,一长为L的不可伸长的不导电细线的一端连着一个质量为m的带电量为q小球,另一端固定于O点,小球恰能静止于电场中A点,OA连线与竖直向成θ角且θ=37°.现把小球拉起至细线成水平方向(如图中虚线OB所示),然后无初速释放.(取sin37°=0.6,cos37°=0.8)求:(1)匀强电场电场强度的大小;
(2)细线到达竖直方向时细线对小球的拉力;
(3)小球经过A点时的速度.
分析:根据小球在A点受重力,拉力,电场力三力平衡,即可求出场强大小;
根据动能定理研究小球从释放到竖直方向即最低点的过程求出小球到最低点的速度;经过最低点时,由重力和细线的拉力的合力提供小球的向心力,由牛顿第二定律求出细线对小球的拉力.
根据动能定理求出小球经过A点的速度.
根据动能定理研究小球从释放到竖直方向即最低点的过程求出小球到最低点的速度;经过最低点时,由重力和细线的拉力的合力提供小球的向心力,由牛顿第二定律求出细线对小球的拉力.
根据动能定理求出小球经过A点的速度.
解答:解:(1)小球恰好能静止与电场中A点,对小球受力分析,如图所示:小球受水平向右的电场力,竖直向下的重力,和斜向上的拉力

可得:F=mgtanθ
又:F=qE
解得:E=
=
;
(2)小球从水平位置到竖直方向的过程中重力和电场力做功,根据动能定理得:
mgL-qEL=
mv2 ①
小球在最低点时时绳子的拉力与重力的和提供向心力:
T-mg=
②
联立①②式,解得:T=
mg
(3)由动能定理,可得:mgLcosθ-qEL(1-sinθ)=
m
解得:vA=
答:(1)匀强电场电场强度的大小为
;
(2)细线到达竖直方向时细线对小球的拉力为
mg;
(3)小球经过A点时的速度为
.

可得:F=mgtanθ
又:F=qE
解得:E=
| mgtanθ |
| q |
| 3mg |
| 4q |
(2)小球从水平位置到竖直方向的过程中重力和电场力做功,根据动能定理得:
mgL-qEL=
| 1 |
| 2 |
小球在最低点时时绳子的拉力与重力的和提供向心力:
T-mg=
| mv2 |
| L |
联立①②式,解得:T=
| 3 |
| 2 |
(3)由动能定理,可得:mgLcosθ-qEL(1-sinθ)=
| 1 |
| 2 |
| v | 2 A |
解得:vA=
| gL |
答:(1)匀强电场电场强度的大小为
| 3mg |
| 4q |
(2)细线到达竖直方向时细线对小球的拉力为
| 3 |
| 2 |
(3)小球经过A点时的速度为
| gL |
点评:本题是带电物体在电场中圆周运动问题,动能定理和向心力结合是常用的解题方法.常见的题型.对于多过程的问题可能多次应用动能定理求解问题.

练习册系列答案
相关题目
 如图所示,在方向水平向左的匀速电场中有一倾角为60°、高为H的固定绝缘斜面体,现将一质量为m,带正电且电荷量为q的小物块(可视为质点)从斜面体顶端由静止释放,已知重力加速度为g,匀强电场的电场强度大小为E=
如图所示,在方向水平向左的匀速电场中有一倾角为60°、高为H的固定绝缘斜面体,现将一质量为m,带正电且电荷量为q的小物块(可视为质点)从斜面体顶端由静止释放,已知重力加速度为g,匀强电场的电场强度大小为E=
| ||
| q |
| A、小物块将沿斜面下滑 | ||
| B、小物块将做曲线运动 | ||
C、小物块到达地面时的速度大小为2
| ||
| D、若其他条件不变,只增大电场强度,小物块到达地面前的运动时间将增大 |
 如图所示,在方向水平向右、大小为E=6×103 N/C的匀强电场中有一个光滑的绝缘平面.一根绝缘细绳两端分别系有带电滑块甲和乙,甲的质量为m1=2×10-4 kg,带电量为q1=2×10-9 C,乙的质量为m2=1×10-4 kg,带电量为q2=-1×10-9 C.开始时细绳处于拉直状态.由静止释放两滑块,t=3s时细绳突然断裂,不计滑块间的库仑力,试求:
如图所示,在方向水平向右、大小为E=6×103 N/C的匀强电场中有一个光滑的绝缘平面.一根绝缘细绳两端分别系有带电滑块甲和乙,甲的质量为m1=2×10-4 kg,带电量为q1=2×10-9 C,乙的质量为m2=1×10-4 kg,带电量为q2=-1×10-9 C.开始时细绳处于拉直状态.由静止释放两滑块,t=3s时细绳突然断裂,不计滑块间的库仑力,试求: (2012?昆明模拟)如图所示,在方向水平的匀强电场中,一个不可伸长的不导电轻细线的一端连着一个质量为m的带电小球,另一端固定于O点,把小球拉直至细线与电场方向平行,然后无初速释放,已知小球摆到最低点的另一侧,线与竖直方向的最大夹角为θ.求小球经过最低点时细线对小球的拉力.
(2012?昆明模拟)如图所示,在方向水平的匀强电场中,一个不可伸长的不导电轻细线的一端连着一个质量为m的带电小球,另一端固定于O点,把小球拉直至细线与电场方向平行,然后无初速释放,已知小球摆到最低点的另一侧,线与竖直方向的最大夹角为θ.求小球经过最低点时细线对小球的拉力. 如图所示,在方向水平向右的匀强电场中,一不可伸长的不导电细线的一端连着一个质量为m的带电小球,另一端固定于O点,当小球静止在B点时,细线与竖直方向夹角θ=30°问:
如图所示,在方向水平向右的匀强电场中,一不可伸长的不导电细线的一端连着一个质量为m的带电小球,另一端固定于O点,当小球静止在B点时,细线与竖直方向夹角θ=30°问: