题目内容
16.位移传感器由发射器和接收器组成,发射器内装有红外线和超声波发射器,接收器内装有红外线和超声波接收器.
(1)如图1,固定在被测运动物体上的发射器向接收器同时发射一个红外线脉冲和一个超声波脉冲,接收器收到红外线脉冲时开始计时t1,收到超声波脉冲时停止计时t2.已知超声波在空气中的传播速度为v(红外线传播时间极短,可忽略),发射器和接收器之间的距离s=v(t2-t1).
(2)某小组设计了使用位移传感器的图2示实验装置测量木块下滑的加速度,让木块从倾斜木板上一点A静止释放,计算机描绘了滑块相对传感器的位移随时间变化规律如图3所示.根据图线计算t0时刻速度v=$\frac{{s}_{0}-{s}_{2}}{2{t}_{0}}$,木块加速度a=$\frac{2{s}_{1}-{s}_{2}-{s}_{0}}{{t}_{0}^{2}}$(用图中给出的s0、s1、s2、t0表示).
分析 (1)由于超声波是匀速运动,由s=vt可得发射器和接收器之间的距离.
(2)由于滑块在斜面上做匀加速直线运动,所以某段时间内的平均速度等于这段时间内中点时刻的瞬时速度;根据加速度的定义式即可求出加速度;
解答 解:(1)超声波是匀速运动,故发射器和接收器之间的距离为:s=vt=v(t2-t1).
(2)根据某段时间内的平均速度等于这段时间内中点时刻的瞬时速度,得:
v1=$\frac{{s}_{0}-{s}_{2}}{2{t}_{0}}$;
木块的加速度:a=$\frac{△x}{{t}^{2}}$=-$\frac{({s}_{0}-{s}_{1})-({s}_{1}-{s}_{2})}{{t}_{0}^{2}}$=$\frac{2{s}_{1}-{s}_{2}-{s}_{0}}{{t}_{0}^{2}}$;
故答案为:
(1)v(t2-t1).
(2)$\frac{{s}_{0}-{s}_{2}}{2{t}_{0}}$,$\frac{2{s}_{1}-{s}_{2}-{s}_{0}}{{t}_{0}^{2}}$.
点评 该题的关键是要分析出物体做匀加速运动,由此才能得出瞬时速度等于平均速度.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
4. 如图所示,平行导轨间距为d,一端跨接一个阻值为R的电阻,匀强磁场的磁感应强度为B,方向与导轨所在平面垂直.一根足够长的金属棒与导轨成θ角放置,金属棒与导轨的电阻不计.当金属棒沿垂直于棒的方向以速度v滑行时,通过电阻R的电流强度是( )
如图所示,平行导轨间距为d,一端跨接一个阻值为R的电阻,匀强磁场的磁感应强度为B,方向与导轨所在平面垂直.一根足够长的金属棒与导轨成θ角放置,金属棒与导轨的电阻不计.当金属棒沿垂直于棒的方向以速度v滑行时,通过电阻R的电流强度是( )
 如图所示,平行导轨间距为d,一端跨接一个阻值为R的电阻,匀强磁场的磁感应强度为B,方向与导轨所在平面垂直.一根足够长的金属棒与导轨成θ角放置,金属棒与导轨的电阻不计.当金属棒沿垂直于棒的方向以速度v滑行时,通过电阻R的电流强度是( )
如图所示,平行导轨间距为d,一端跨接一个阻值为R的电阻,匀强磁场的磁感应强度为B,方向与导轨所在平面垂直.一根足够长的金属棒与导轨成θ角放置,金属棒与导轨的电阻不计.当金属棒沿垂直于棒的方向以速度v滑行时,通过电阻R的电流强度是( )| A. | $\frac{Bdv}{R}$ | B. | $\frac{Bdvsinθ}{R}$ | C. | $\frac{Bdvcosθ}{R}$ | D. | $\frac{Bdv}{Rsinθ}$ |
1.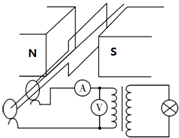 今有某小型发电机和一理想变压器连接后给一个灯泡供电,电路如图(电压表和电流表均为理想电表).已知该发电机线圈匝数为N,电阻为r,当线圈以转速n匀速转动时,电压表示数为U,灯泡(额定电压为U0.电阻恒为R)恰能正常发光,则( )
今有某小型发电机和一理想变压器连接后给一个灯泡供电,电路如图(电压表和电流表均为理想电表).已知该发电机线圈匝数为N,电阻为r,当线圈以转速n匀速转动时,电压表示数为U,灯泡(额定电压为U0.电阻恒为R)恰能正常发光,则( )
 今有某小型发电机和一理想变压器连接后给一个灯泡供电,电路如图(电压表和电流表均为理想电表).已知该发电机线圈匝数为N,电阻为r,当线圈以转速n匀速转动时,电压表示数为U,灯泡(额定电压为U0.电阻恒为R)恰能正常发光,则( )
今有某小型发电机和一理想变压器连接后给一个灯泡供电,电路如图(电压表和电流表均为理想电表).已知该发电机线圈匝数为N,电阻为r,当线圈以转速n匀速转动时,电压表示数为U,灯泡(额定电压为U0.电阻恒为R)恰能正常发光,则( )| A. | 变压器的匝数比为U:U0 | |
| B. | 电流表的示数为$\frac{{{U}_{0}}^{2}}{RU}$ | |
| C. | 在图示位置时,发电机线圈的磁通量为$\frac{{\sqrt{2}U}}{2Nnπ}$ | |
| D. | 从图示位置开始计时,变压器输入电压的瞬时值表达式为u=Usin2nπt |
5.用油膜法测出油分子的直径后,要测定阿伏加德罗常数,只需知道油滴的( )
| A. | 摩尔质量 | B. | 摩尔体积 | C. | 体积 | D. | 密度 |
6.下列说法正确的是( )
| A. | 匀速圆周运动是一种匀速运动 | |
| B. | 匀速圆周运动是一种匀变速运动 | |
| C. | 匀速圆周运动是一种变加速运动 | |
| D. | 物体做圆周运动时,其合力垂直于速度方向 |

 如图,用一绳子a把物体挂起来,再用另一根水平的绳子b 把物体拉向一旁固定起来.物体的重力是60N,绳子a与竖直方向的夹角θ=37°,绳子a与b对物体的拉力分别是多大?(sin37°=0.6,cos37°=0.8)
如图,用一绳子a把物体挂起来,再用另一根水平的绳子b 把物体拉向一旁固定起来.物体的重力是60N,绳子a与竖直方向的夹角θ=37°,绳子a与b对物体的拉力分别是多大?(sin37°=0.6,cos37°=0.8)
 如图所示,点光源S到平面镜M的距离为d=0.5m.光屏AB与平面镜的初始位置平行.当平面镜M绕垂直于纸面过中心O的转轴以ω=4rad/s的角速度逆时针匀速转过300时,垂直射向平面镜的光线SO在光屏上的光斑P的移动速度大小是多少?
如图所示,点光源S到平面镜M的距离为d=0.5m.光屏AB与平面镜的初始位置平行.当平面镜M绕垂直于纸面过中心O的转轴以ω=4rad/s的角速度逆时针匀速转过300时,垂直射向平面镜的光线SO在光屏上的光斑P的移动速度大小是多少?