题目内容
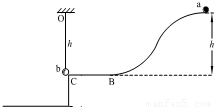
如图,质量为m的b球用长h的细绳悬挂于水平轨道BC的出口C处.质量也为m的小球a,从距BC高h的A处由静止释放,沿ABC光滑轨道滑下,在C处与b球正碰并与b粘在一起.已知BC轨道距地面有一定的高度,悬挂b球的细绳能承受的最大拉力为2.8mg.试问:①a与b球碰前瞬间,a球的速度多大?②a、b两球碰后,细绳是否会断裂?(要求通过计算回答)
【答案】分析:(1)以a球为研究对象,由动能定理可以求出a与b两球碰撞前a球的速度.
(2)a与b碰撞过程中动量守恒,由动量守恒定律求出碰后的速度,
然后它们做圆周运动,由牛顿第二定律列方程,求出绳子的拉力,然后判断绳子是否会断裂.
解答:解:①以a球为研究对象,在a求下滑到C点过程中,
由动能定理可得,mgh= mv2-0,解得:a的速度v=
mv2-0,解得:a的速度v= ;
;
②a与b两球碰撞过程动量守恒,
由动量守恒得:mv=(m+m)v′,
解得:v′=
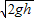 ;
;
两小球做圆周运动,
由牛顿第二定律可得:F-2mg=2m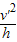 ,
,
解得F=3mg,F=3mg>2.8mg,细绳会断裂.
答::①a与b球碰前瞬间,a球的速度为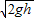 .
.
②a、b两球碰后,细绳会断裂.
点评:应用动能定理、动量守恒定律、牛顿第二定律即可解题,本题难度不大;第一问也可以应用机械能守恒定律解题.
(2)a与b碰撞过程中动量守恒,由动量守恒定律求出碰后的速度,
然后它们做圆周运动,由牛顿第二定律列方程,求出绳子的拉力,然后判断绳子是否会断裂.
解答:解:①以a球为研究对象,在a求下滑到C点过程中,
由动能定理可得,mgh=
 mv2-0,解得:a的速度v=
mv2-0,解得:a的速度v= ;
; ②a与b两球碰撞过程动量守恒,
由动量守恒得:mv=(m+m)v′,
解得:v′=

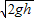 ;
;两小球做圆周运动,
由牛顿第二定律可得:F-2mg=2m
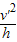 ,
,解得F=3mg,F=3mg>2.8mg,细绳会断裂.
答::①a与b球碰前瞬间,a球的速度为
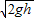 .
.②a、b两球碰后,细绳会断裂.
点评:应用动能定理、动量守恒定律、牛顿第二定律即可解题,本题难度不大;第一问也可以应用机械能守恒定律解题.

练习册系列答案
相关题目
 (2012?湖南模拟)如图,质量为m的b球用长h的细绳悬挂于水平轨道BC的出口C处.质量也为m的小球a,从距BC高h的A处由静止释放,沿ABC光滑轨道滑下,在C处与b球正碰并与b粘在一起.已知BC轨道距地面有一定的高度,悬挂b球的细绳能承受的最大拉力为2.8mg.试问:①a与b球碰前瞬间,a球的速度多大?
(2012?湖南模拟)如图,质量为m的b球用长h的细绳悬挂于水平轨道BC的出口C处.质量也为m的小球a,从距BC高h的A处由静止释放,沿ABC光滑轨道滑下,在C处与b球正碰并与b粘在一起.已知BC轨道距地面有一定的高度,悬挂b球的细绳能承受的最大拉力为2.8mg.试问:①a与b球碰前瞬间,a球的速度多大? (2013?南开区一模)如图,质量为m的b球用长h的细绳悬挂于水平轨道BC的出口C处.质量也为m的小球a,从距BC高h的A处由静止释放,沿ABC光滑轨道滑下,在C处与b球正碰并与b粘在一起.已知BC轨道距地面的高度为0.5h,悬挂b球的细绳能承受的最大拉力为2.8mg.试问:
(2013?南开区一模)如图,质量为m的b球用长h的细绳悬挂于水平轨道BC的出口C处.质量也为m的小球a,从距BC高h的A处由静止释放,沿ABC光滑轨道滑下,在C处与b球正碰并与b粘在一起.已知BC轨道距地面的高度为0.5h,悬挂b球的细绳能承受的最大拉力为2.8mg.试问: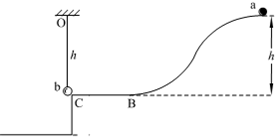 (1)以下说法正确的是
(1)以下说法正确的是 物理--选修3-5
物理--选修3-5