题目内容
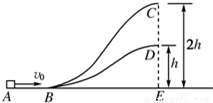
如图所示,ABC和ABD为两个光滑固定轨道,A、B、E在同一水平面上,C、D、E在同一竖直线上,D点距水平面的高度为h,C点的高度为2h,一滑块从A点以初速度v分别沿两轨道滑行到C或D处后水平抛出.(1)求滑块落到水平面时,落点与E点间的距离xC和xD;
(2)为实现xC>xD,v应满足什么条件?
(3)如果滑块的初速度一定,要使它从最高点抛出后的水平射程最大,则h′应为多大?此时的水平射程为多少?
【答案】分析:(1)滑块离开C和D后,做平抛运动,由平抛运动的规律可以求的水平的位移;
(2)根据(1)中求得sC和sD的大小的表达式,根据题意分析可以得出,v应满足的条件.
(3)根据(1)中求得的水平位移,应用数学知识求出水平位移的最大条件,并求出最大水平位移.
解答:解:(1)设抛出点高度为y,根据机械能守恒 mv2=
mv2= mv2+mgy,
mv2+mgy,
所以平抛的初速度为 v=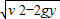 ,
,
平抛后物体在竖直方向上做自由落体运动,
所以落地时间t满足 y= gt2,
gt2,
所以 t=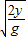 ,
,
落地点离抛出点的水平距离s=vt=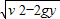
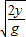 ,
,
分别以y=2h和y=h代入得:
sC=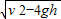
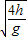 ,
,
sD=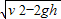
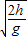 ,
,
(2)由题意知,要使sC<sD,
也就是要有2(v2-4gh)<v2-2gh,
所以v2<6gh,
又滑块必须能到达C点,
即 vC2=v2-4gh,
所以 v2>4gh,
因此初速度应满足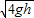 <v<
<v<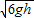 .
.
(3)由(1)可知,落地点离抛出点的水平距离:
s=vt=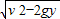
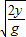 =
=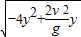 =
=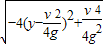 ,
,
当y=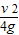 ,即h′=
,即h′=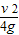 时,滑块的水平射程最大,为smax=
时,滑块的水平射程最大,为smax=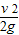 ;
;
答:(1)滑块落到水平面时,落点与E点间的距离 sC=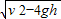
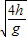 ,sD=
,sD=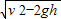
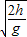 ;
;
(2)初速度应满足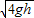 <v<
<v<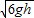 .
.
(3)当h′=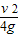 时,滑块的水平射程最大为
时,滑块的水平射程最大为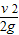 .
.
点评:整个过程中,物体的机械能守恒,离开C和D后物体做平抛运动,根据平抛运动的规律分析可以得出结论.
(2)根据(1)中求得sC和sD的大小的表达式,根据题意分析可以得出,v应满足的条件.
(3)根据(1)中求得的水平位移,应用数学知识求出水平位移的最大条件,并求出最大水平位移.
解答:解:(1)设抛出点高度为y,根据机械能守恒
 mv2=
mv2= mv2+mgy,
mv2+mgy,所以平抛的初速度为 v=
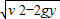 ,
,平抛后物体在竖直方向上做自由落体运动,
所以落地时间t满足 y=
 gt2,
gt2,所以 t=
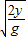 ,
,落地点离抛出点的水平距离s=vt=
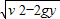
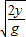 ,
,分别以y=2h和y=h代入得:
sC=
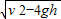
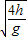 ,
,sD=
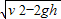
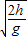 ,
,(2)由题意知,要使sC<sD,
也就是要有2(v2-4gh)<v2-2gh,
所以v2<6gh,
又滑块必须能到达C点,
即 vC2=v2-4gh,
所以 v2>4gh,
因此初速度应满足
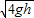 <v<
<v<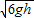 .
.(3)由(1)可知,落地点离抛出点的水平距离:
s=vt=
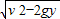
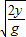 =
=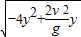 =
=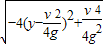 ,
,当y=
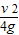 ,即h′=
,即h′=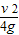 时,滑块的水平射程最大,为smax=
时,滑块的水平射程最大,为smax=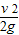 ;
;答:(1)滑块落到水平面时,落点与E点间的距离 sC=
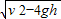
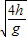 ,sD=
,sD=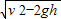
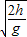 ;
;(2)初速度应满足
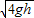 <v<
<v<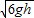 .
.(3)当h′=
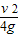 时,滑块的水平射程最大为
时,滑块的水平射程最大为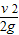 .
.点评:整个过程中,物体的机械能守恒,离开C和D后物体做平抛运动,根据平抛运动的规律分析可以得出结论.

练习册系列答案
相关题目
 (2005?闵行区二模)本题中A.B分别为一期教材、二期新教材分叉题,考生选择只能选A组的全部或B组的全部完成
(2005?闵行区二模)本题中A.B分别为一期教材、二期新教材分叉题,考生选择只能选A组的全部或B组的全部完成 如图所示,ABC和ABD为两个光滑固定轨道,A、B、E在同一水平面上,C、D、E在同一竖直线上,D点距水平面的高度为h,C点的高度为2h,一滑块从A点以初速度v0分别沿两轨道滑行到C或D处后水平抛出.
如图所示,ABC和ABD为两个光滑固定轨道,A、B、E在同一水平面上,C、D、E在同一竖直线上,D点距水平面的高度为h,C点的高度为2h,一滑块从A点以初速度v0分别沿两轨道滑行到C或D处后水平抛出. 如图所示,ABC和DEF是在同一竖直平面内的两条光滑轨道,其中ABC的末端水平,DEF是半径为r=0.4m的半圆形轨道,其直径DF沿竖直方向,C、D可看作重合.现有一质量m=0.1kg,可视为质点的小球从轨道ABC上的A点由静止释放,若小球经C处后恰能沿轨道DEF做圆周运动,(取g=10m/s2),求:
如图所示,ABC和DEF是在同一竖直平面内的两条光滑轨道,其中ABC的末端水平,DEF是半径为r=0.4m的半圆形轨道,其直径DF沿竖直方向,C、D可看作重合.现有一质量m=0.1kg,可视为质点的小球从轨道ABC上的A点由静止释放,若小球经C处后恰能沿轨道DEF做圆周运动,(取g=10m/s2),求: 如图所示,ABC和DEF是在同一竖直平面内的两条光滑轨道,其中ABC的末端水平,DEF是半径为r=0.4m的半圆形轨道,其直径DF沿竖直方向,C、D可看作重合.现有一可视为质点的小球从轨道ABC上距C点高为H的地方由静止释放,g取10m/s2.以下说法正确的是( )
如图所示,ABC和DEF是在同一竖直平面内的两条光滑轨道,其中ABC的末端水平,DEF是半径为r=0.4m的半圆形轨道,其直径DF沿竖直方向,C、D可看作重合.现有一可视为质点的小球从轨道ABC上距C点高为H的地方由静止释放,g取10m/s2.以下说法正确的是( ) 如图所示,ABC和DEF为同种材料构成的柱形透明体的横截面,其中ABC部分为等腰直角三角形,DEF部分为半圆形,其间有一条小的缝隙.一束单色平行光从真空垂直射向AB或AC面,材料的折射率n=1.6.下列说法中正确的是( )
如图所示,ABC和DEF为同种材料构成的柱形透明体的横截面,其中ABC部分为等腰直角三角形,DEF部分为半圆形,其间有一条小的缝隙.一束单色平行光从真空垂直射向AB或AC面,材料的折射率n=1.6.下列说法中正确的是( )