题目内容
10. 如图所示,质量为2.0×103 kg的汽车在水平公路上行驶,当汽车经过半径为60m的弯路时,车速为20m/s.此时汽车转弯所需要的向心力大小为多大?若轮胎与路面间的最大静摩擦力为3×104 N,计算安全拐弯的速度不能超过多大?(保留两位有效数字)
如图所示,质量为2.0×103 kg的汽车在水平公路上行驶,当汽车经过半径为60m的弯路时,车速为20m/s.此时汽车转弯所需要的向心力大小为多大?若轮胎与路面间的最大静摩擦力为3×104 N,计算安全拐弯的速度不能超过多大?(保留两位有效数字)
分析 根据向心力公式求出汽车转弯时所需要的向心力,根据最大静摩擦力提供向心力求出汽车安全拐弯的速度.
解答 解:汽车转弯所需要的向心力Fn=m$\frac{{v}^{2}}{R}$=2×103×$\frac{2{0}^{2}}{60}$ N≈1.3×104 N.
由fm=m$\frac{{{v}_{m}}^{2}}{R}$得,汽车拐弯的最大速度${v}_{m}=\sqrt{\frac{{f}_{m}R}{m}}=\sqrt{\frac{3×1{0}^{4}×60}{2×1{0}^{3}}}$m/s=30m/s.
答:汽车转弯所需要的向心力大小为1.3×104 N,安全拐弯的速度不能超过30m/s.
点评 解决本题的关键知道汽车拐弯向心力的来源,结合牛顿第二定律进行求解,基础题.

练习册系列答案
相关题目
20.假设一个沿着一定方向运动的光子和一个静止的自由电子相互碰撞以后,电子向某一个方向运动,光子沿另一方向散射出去,则这个散射光子跟原来的光子相比( )
| A. | 波长变长 | B. | 速度变小 | C. | 光子能量变小 | D. | 频率变大 |
1.某短跑运动员参加100m竞赛,测得他在50m处的速度为6m/s,10s末到达终点时的速度为8m/s,则以下说法中正确的是( )
| A. | 运动员全程的平均速度是11m/s | B. | 8m/s指平均速度 | ||
| C. | 运动员全程的平均速度是7m/s | D. | 6m/s指瞬时速度 |
18. 如图所示,轰炸机沿水平方向以90m/s的速度匀速飞行,到达山坡底端正上方时释放一颗炸弹,并垂直击中山坡上的目标A.已知山坡倾角θ=37°,(g=10m/s2,sin37°=0.6,cos37°=0.8),由此可算出( )
如图所示,轰炸机沿水平方向以90m/s的速度匀速飞行,到达山坡底端正上方时释放一颗炸弹,并垂直击中山坡上的目标A.已知山坡倾角θ=37°,(g=10m/s2,sin37°=0.6,cos37°=0.8),由此可算出( )
 如图所示,轰炸机沿水平方向以90m/s的速度匀速飞行,到达山坡底端正上方时释放一颗炸弹,并垂直击中山坡上的目标A.已知山坡倾角θ=37°,(g=10m/s2,sin37°=0.6,cos37°=0.8),由此可算出( )
如图所示,轰炸机沿水平方向以90m/s的速度匀速飞行,到达山坡底端正上方时释放一颗炸弹,并垂直击中山坡上的目标A.已知山坡倾角θ=37°,(g=10m/s2,sin37°=0.6,cos37°=0.8),由此可算出( )| A. | 炸弹离开飞机后飞行的水平位移为1000m | |
| B. | 炸弹击中A点瞬间的速度与水平方向的夹角为37° | |
| C. | 炸弹离开飞机后的飞行时间为12s | |
| D. | 炸弹离开飞机后飞行的竖直位移为720m |
5.关于弹簧的弹性势能,下列说法不正确的是( )
| A. | 弹簧的弹性势能跟拉伸(或压缩)的长度有关 | |
| B. | 弹簧的弹性势能跟弹簧的劲度系数有关 | |
| C. | 同一弹簧,在弹性限度内,形变量越大,弹性势能越大 | |
| D. | 弹性势能的大小跟使弹簧发生形变的物体有关 |
15.A、B两物体在光滑水平面上沿同一直线运动,发生碰撞前后的v-t图线如图所示,由图线可以判断( )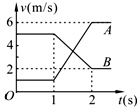

| A. | A、B的动量变化量一定相同 | |
| B. | A、B的质量之比为5:3 | |
| C. | A的动能增加量一定等于B的动能减少量 | |
| D. | A对B做多少负功,B对A就做多少正功 |
2. 如图所示,在绕竖直轴做匀速圆周运动的圆筒内壁上紧靠着一个物体和筒一起转动,维持物体做圆周运动的向心力是( )
如图所示,在绕竖直轴做匀速圆周运动的圆筒内壁上紧靠着一个物体和筒一起转动,维持物体做圆周运动的向心力是( )
 如图所示,在绕竖直轴做匀速圆周运动的圆筒内壁上紧靠着一个物体和筒一起转动,维持物体做圆周运动的向心力是( )
如图所示,在绕竖直轴做匀速圆周运动的圆筒内壁上紧靠着一个物体和筒一起转动,维持物体做圆周运动的向心力是( )| A. | 重力 | B. | 弹力 | C. | 静摩擦力 | D. | 滑动摩擦力 |
19.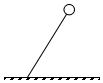 如图所示,在匀强电场中,绝缘丝线一端固定于地面,另一端系住一个带电小球,张紧的丝线使小球处于静止状态.忽略空气阻力,剪断丝线后小球将做( )
如图所示,在匀强电场中,绝缘丝线一端固定于地面,另一端系住一个带电小球,张紧的丝线使小球处于静止状态.忽略空气阻力,剪断丝线后小球将做( )
 如图所示,在匀强电场中,绝缘丝线一端固定于地面,另一端系住一个带电小球,张紧的丝线使小球处于静止状态.忽略空气阻力,剪断丝线后小球将做( )
如图所示,在匀强电场中,绝缘丝线一端固定于地面,另一端系住一个带电小球,张紧的丝线使小球处于静止状态.忽略空气阻力,剪断丝线后小球将做( )| A. | 类平抛运动 | B. | 匀速圆周运动 | C. | 匀加速直线运动 | D. | 变加速曲线运动 |
 如图所示,边长为L的正方形导线框abcd以初速度v沿光滑水平面进入宽度为S(S>L)、方向竖直向下与线框平面垂直的匀强有界磁场.如果bc边刚进入磁场时通过导线框的电流强度为i0,则在下列选项所示的四幅反映通过线框电流i随其对O点位移x变化的图象中,可能正确的是( )
如图所示,边长为L的正方形导线框abcd以初速度v沿光滑水平面进入宽度为S(S>L)、方向竖直向下与线框平面垂直的匀强有界磁场.如果bc边刚进入磁场时通过导线框的电流强度为i0,则在下列选项所示的四幅反映通过线框电流i随其对O点位移x变化的图象中,可能正确的是( )


