题目内容
11.天文学中把两颗距离比较近,又与其它星体距离比较远的星体叫做双星,双星的间距是一定的.设双星质量分别是m1、m2,球心间距为L.则质量为m1星体的运行的周期是$2π\sqrt{\frac{{L}^{3}}{G({m}_{1}+{m}_{2})}}$,速度是${m_2}\sqrt{\frac{G}{{({m_1}+{m_2}){L^\;}}}}$.分析 双星靠相互间的万有引力提供向心力,抓住角速度相等,向心力相等求出轨道半径之比,进一步计算轨道半径大小;据万有引力提供向心力计算出周期;最后根据v=$\frac{2πr}{T}$求解线速度.
解答 解:设双星中质量为m1的天体轨道半径为r1,质量为m2的天体轨道半径为r2
据万有引力定律和牛顿第二定律,得:
$\frac{{G{m_1}{m_2}}}{L^2}={m_1}{ω^2}{r_1}$…①
$\frac{{G{m_1}{m_2}}}{L^2}={m_2}{ω^2}{r_2}$…②
r1+r2=L…③
由①②③联立解得:
${r_1}=\frac{{{m_2}L}}{{{m_1}+{m_2}}}$,
${r_2}=\frac{{{m_1}L}}{{{m_1}+{m_2}}}$,
再由:$\frac{{G{m_1}{m_2}}}{L^2}={m_1}{(\frac{2π}{T})^2}{r_1}$,得:
运行的周期:T=$2π\sqrt{\frac{L^3}{{G({m_1}+{m_2})}}}$
质量为m1星体的线速度:${v}_{1}=\frac{2π{r}_{1}}{T}$=$\frac{{2π\frac{{{m_2}L}}{{{m_1}+{m_2}}}}}{{2π\sqrt{\frac{L^3}{{G({m_1}+{m_2})}}}}}={m_2}\sqrt{\frac{G}{{({m_1}+{m_2}){L^\;}}}}$
故答案为:$2π\sqrt{\frac{{L}^{3}}{G({m}_{1}+{m}_{2})}}$,${m_2}\sqrt{\frac{G}{{({m_1}+{m_2}){L^\;}}}}$.
点评 解决本题的关键掌握双星模型系统,知道它们靠相互间的万有引力提供向心力,向心力的大小相等,角速度的大小相等.

 在如图所示的电路中,灯泡L的电阻大于电源的内阻r,闭合电键S,将滑动变阻器滑片P向左移动一段距离后,下列结论正确的是( )
在如图所示的电路中,灯泡L的电阻大于电源的内阻r,闭合电键S,将滑动变阻器滑片P向左移动一段距离后,下列结论正确的是( )| A. | 电容器C上电荷量增大 | B. | 电源的输出功率变大 | ||
| C. | 灯泡L变暗 | D. | 电流表读数变小,电压表读数变大 |
| A. | 20m | B. | 30m | C. | 40m | D. | 50m |
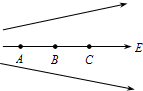 如图所示,实线为电场线,且AB=BC,电场中的A、B、C三点的场强分别为EA、EB、EC,电势分别为φA、φB、φC,AB、BC间的电势差分别为UAB、UBC.下列关系中正确的有( )
如图所示,实线为电场线,且AB=BC,电场中的A、B、C三点的场强分别为EA、EB、EC,电势分别为φA、φB、φC,AB、BC间的电势差分别为UAB、UBC.下列关系中正确的有( )| A. | EA>EB>EC | B. | φA>φB>φC | C. | UAB=UBC | D. | UAB<UBC |
| A. | α粒子散射实验说明了原子的全部正电荷和绝大部分质量集中在一个很小的核上 | |
| B. | 原子核外电子吸收能量脱离原子核束缚形成β射线 | |
| C. | 两个质子与两个中子的质量之和等于${\;}_{2}^{4}$He原子核的质量 | |
| D. | 氢原子从激发态向基态跃迁只能辐射特定频率的光子 |
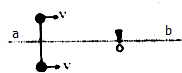 在光滑的水平桌面上,两个质量均为m小球用长为2L结实细而轻的细绳连接,细绳刚好伸直且无张力,两个小球一相同的速度v=$\sqrt{gL}$向右做匀速直线运动,ab是细绳的垂直平分线,在ab上的O点固定一个光滑小钉,细绳被小钉挡住后,两小球在即将碰撞的瞬间,细绳对小钉的作用力大小为( )
在光滑的水平桌面上,两个质量均为m小球用长为2L结实细而轻的细绳连接,细绳刚好伸直且无张力,两个小球一相同的速度v=$\sqrt{gL}$向右做匀速直线运动,ab是细绳的垂直平分线,在ab上的O点固定一个光滑小钉,细绳被小钉挡住后,两小球在即将碰撞的瞬间,细绳对小钉的作用力大小为( )| A. | mg | B. | 2mg | C. | 3mg | D. | 4mg |
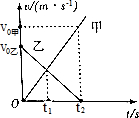 如图所示,为甲、乙两物体的v-t图象,则以下说法中正确的是( )
如图所示,为甲、乙两物体的v-t图象,则以下说法中正确的是( )| A. | 甲做匀加速直线运动,乙做匀减速直线运动 | |
| B. | 若甲、乙两物体在同一直线上运动,则两物体一定不会相遇 | |
| C. | 甲、乙两物体的加速度大小一定相等,方向相反 | |
| D. | 在t1~t2的时间内,甲、乙两物体发生的位移一样 |
| A. |  子弹出枪膛时的速度 | B. |  地球的自转 | ||
| C. |  跳水运动员的动作 | D. |  乒乓球的旋转速度 |
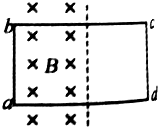 单匝线圈abcd水平放置,有一半面积处在竖直向下的匀强磁场中,如图所示,线圈面积为S,磁感应强度为B,当线圈绕ab边从图示位置转过30°和60°时,穿过线圈的磁通量分别是多少?
单匝线圈abcd水平放置,有一半面积处在竖直向下的匀强磁场中,如图所示,线圈面积为S,磁感应强度为B,当线圈绕ab边从图示位置转过30°和60°时,穿过线圈的磁通量分别是多少?