题目内容
3. 我国“神舟十号”飞船已于2013年6月11日17时38分成功发射,并与“天宫一号”目标飞行器成功交会对接,飞行乘组由3名航天员组成,假设“神舟十号”在飞行的过程中绕地球做圆周运动,已知地球的半径为R,地球的表面的重力加速度为g,飞船绕地球运行的周期为T.求:
我国“神舟十号”飞船已于2013年6月11日17时38分成功发射,并与“天宫一号”目标飞行器成功交会对接,飞行乘组由3名航天员组成,假设“神舟十号”在飞行的过程中绕地球做圆周运动,已知地球的半径为R,地球的表面的重力加速度为g,飞船绕地球运行的周期为T.求:(1)飞船离地面的高度h;
(2)如图所示,卫星A与“神舟十号”B在同一轨道平面,已知卫星A的运行方向与B相同,A的轨道为B的轨道的2倍,某时刻A、B相距最近,则至少经过多长时间它们再一次相距最近?
分析 根据万有引力提供向心力,以及万有引力等于重力求出飞船离地面的高度h.
某时刻两卫星正好同时通过地面上同一点的正上方,当两颗卫星转动角度相差2π时,即A比B多转一圈,相距最近.
解答 解:(1)根据万有引力等于重力得,$G\frac{Mm}{{R}^{2}}=mg$
解得GM=gR2.
根据万有引力提供向心力得,$G\frac{Mm}{(R+h)^{2}}=m\frac{4{π}^{2}}{{T}^{2}}(R+h)$
解得h=$\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}-R$
(2)根据万有引力提供向心力$G\frac{Mm}{{r}^{2}}=m\frac{4{π}^{2}}{{T}^{2}}r$,得$T=2π\sqrt{\frac{{r}^{3}}{GM}}$
所以$\frac{{T}_{A}}{{T}_{B}}=\sqrt{(\frac{{r}_{A}}{{r}_{B}})^{3}}=\sqrt{(\frac{2}{1})^{3}}$
故${T}_{A}=2\sqrt{2}T$
至少经过时间t它们再一次相距最近,此时A比B多转一圈,
即 $\frac{t}{{T}_{B}}-\frac{t}{{T}_{A}}$=1
即$(\frac{1}{T}-\frac{1}{2\sqrt{2}T})t=1$
解得:t=$\frac{8-2\sqrt{2}}{7}T$
答:(1)飞船离地面的高度h为$\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}-R$;
(2)至少经过$\frac{8-2\sqrt{2}}{7}T$它们再一次相距最近.
点评 本题既可应用万有引力提供向心力求解,也可应用开普勒行星运动定律求解,以后者较为方便,两卫星何时相距最远的求解,用到的数学变换相对较多,增加了本题难度.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案| A. | 1N | B. | 2N | C. | 3N | D. | 4N |
| A. | 原、副线圈匝数比为5:1 | |
| B. | 副线圈中电流的频率是50Hz | |
| C. | 原线圈的导线比副线圈的要粗 | |
| D. | 输入原线圈的电流等于居民小区各用电器电流的总和 |
| A. | 卫星距地面的高度确定 | |
| B. | 卫星的运行轨道在地球的赤道平面内 | |
| C. | 卫星的运行周期与地球的自转周期相同 | |
| D. | 卫星的运行角速度与地球的自转角速度相同 |
 如图所示为新一代炊具--电磁炉,无烟、无明火、无污染,不产生有害气体、高效节能等是磁感线通过含铁质锅底时,即会产生无数小涡流,使锅体本身自行高速发热,然后再加热锅内食物.下列相关说法中正确的是( )
如图所示为新一代炊具--电磁炉,无烟、无明火、无污染,不产生有害气体、高效节能等是磁感线通过含铁质锅底时,即会产生无数小涡流,使锅体本身自行高速发热,然后再加热锅内食物.下列相关说法中正确的是( )| A. | 线圈中可以通以直流电 | |
| B. | 电磁炉的加热功率只跟通入电流频率有关,跟电流大小无关 | |
| C. | 锅体中的涡流是由变化的磁场产生的 | |
| D. | 电磁炉也可用砂锅作为锅体 |
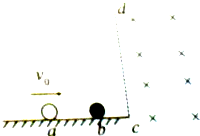 如图所示,在光滑水平面的右侧连接一个相互垂直的匀强电场和匀强磁场,磁场方向垂直纸面向里,其大小为B═0.5T,假设其范围无限大.质量为m=0.1kg的金属黑球静止在水平面的b点,有同种材料制成的白球,其质量与体积与黑球相同,白球以速度v0=10m/s的水平速度射向黑球并发生弹性碰撞,碰后的黑球恰好在cd右侧区域内做匀速圆周运动,已知白球所带电荷量为q=1×10-2C,取g=10m/s2,求:
如图所示,在光滑水平面的右侧连接一个相互垂直的匀强电场和匀强磁场,磁场方向垂直纸面向里,其大小为B═0.5T,假设其范围无限大.质量为m=0.1kg的金属黑球静止在水平面的b点,有同种材料制成的白球,其质量与体积与黑球相同,白球以速度v0=10m/s的水平速度射向黑球并发生弹性碰撞,碰后的黑球恰好在cd右侧区域内做匀速圆周运动,已知白球所带电荷量为q=1×10-2C,取g=10m/s2,求: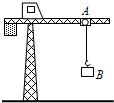 如图,塔吊臂上有一可以沿水平方向运动的小车A,小车下装有吊着物体B的吊钩.在小车A与物体B以相同的水平速度4m/s沿吊臂方向匀速运动的同时,吊钩将物体由静止开始以0.5m/s2的加速度向上匀加速吊起,经过6s后,求物体的位移和速度.
如图,塔吊臂上有一可以沿水平方向运动的小车A,小车下装有吊着物体B的吊钩.在小车A与物体B以相同的水平速度4m/s沿吊臂方向匀速运动的同时,吊钩将物体由静止开始以0.5m/s2的加速度向上匀加速吊起,经过6s后,求物体的位移和速度.