题目内容
17.质子1和质子2垂直进入同一匀强磁场,其速度之比v1:v2=2:1,则两个质子在磁场中做匀速圆周运动的半径之比r1:r2=2:1,周期之比T1:T2=1:1.分析 质子在磁场中做圆周运动,由洛伦兹力提供圆周运动向心力,得到轨道半径和周期表达式,再求解即可.
解答 解:质子在磁场中做匀速圆周运动,由洛伦兹力提供圆周运动向心力,则有:
qvB=m$\frac{{v}^{2}}{r}$
则得轨道半径为:r=$\frac{mv}{qB}$
周期为:T=$\frac{2πr}{v}$=$\frac{2πm}{qB}$,与v无关
根据v1:v2=2:1,
得:r1:r2=2:1,T1:T2=1:1.
由题意:两个带电粒子的周期相同,由上式知荷质比(电量与质量的比值)一定相等,故ABC错误,D正确.
故答案为:2:1,1:1.
点评 根据洛伦兹力提供圆周运动向心力,推导出轨道半径和周期的公式,再运用比例法,即可解答本题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
8. 如图所示,电动机线圈电阻为R,电动机正常工作时,两端的电压为U,通过的电流为I,电源电动势为E,内阻为r,下列说法中正确的是( )
如图所示,电动机线圈电阻为R,电动机正常工作时,两端的电压为U,通过的电流为I,电源电动势为E,内阻为r,下列说法中正确的是( )
 如图所示,电动机线圈电阻为R,电动机正常工作时,两端的电压为U,通过的电流为I,电源电动势为E,内阻为r,下列说法中正确的是( )
如图所示,电动机线圈电阻为R,电动机正常工作时,两端的电压为U,通过的电流为I,电源电动势为E,内阻为r,下列说法中正确的是( )| A. | 电源的总功率为UI | B. | 电动机的输入总功率为UI | ||
| C. | 电动机输出的机械功率为UI-I2R | D. | 电动机线圈产生的热功率为$\frac{{U}^{2}}{R}$ |
5. 如图所示的电路中,电源内阻不可忽略,若调整可变电阻R的阻值,可使电压表
如图所示的电路中,电源内阻不可忽略,若调整可变电阻R的阻值,可使电压表 的示数减小△U(电压表为理想电表),在这个过程中( )
的示数减小△U(电压表为理想电表),在这个过程中( )
 如图所示的电路中,电源内阻不可忽略,若调整可变电阻R的阻值,可使电压表
如图所示的电路中,电源内阻不可忽略,若调整可变电阻R的阻值,可使电压表 的示数减小△U(电压表为理想电表),在这个过程中( )
的示数减小△U(电压表为理想电表),在这个过程中( )| A. | R2两端的电压增加,增加量一定等于△U | |
| B. | 流过R的电流会减小 | |
| C. | 路端电压减小,减少量一定等于△U | |
| D. | △U和干路电流的变化△I的比值保持不变 |
12.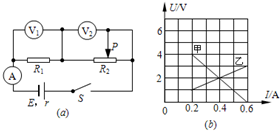 在如图(a)所示的电路中,R1为定值电阻,R2为滑动变阻器.闭合开关S,将滑动变阻器的滑动触头P从最右端滑到最左端,两个电压表(内阻极大)的示数随电路中电流变化的完整过程图线如图(b)所示.则下列说法正确的是( )
在如图(a)所示的电路中,R1为定值电阻,R2为滑动变阻器.闭合开关S,将滑动变阻器的滑动触头P从最右端滑到最左端,两个电压表(内阻极大)的示数随电路中电流变化的完整过程图线如图(b)所示.则下列说法正确的是( )
 在如图(a)所示的电路中,R1为定值电阻,R2为滑动变阻器.闭合开关S,将滑动变阻器的滑动触头P从最右端滑到最左端,两个电压表(内阻极大)的示数随电路中电流变化的完整过程图线如图(b)所示.则下列说法正确的是( )
在如图(a)所示的电路中,R1为定值电阻,R2为滑动变阻器.闭合开关S,将滑动变阻器的滑动触头P从最右端滑到最左端,两个电压表(内阻极大)的示数随电路中电流变化的完整过程图线如图(b)所示.则下列说法正确的是( )| A. | 图线甲是电压表V1示数随电流变化的图线 | |
| B. | 电源内电阻的阻值为5Ω | |
| C. | 电源的最大输出功率为1.5W | |
| D. | 滑动变阻器R2的最大功率为0.9W | |
| E. | 电源电动势为6V |
6. 光滑水平的桌面固定在向前做匀速直线运动的火车车厢内,桌上有相对火车静止的小球,一小朋友面朝火车前进方向坐在桌子旁边,如图所示,当火车突然加速时,小朋友看到小球相对火车的运动是( )
光滑水平的桌面固定在向前做匀速直线运动的火车车厢内,桌上有相对火车静止的小球,一小朋友面朝火车前进方向坐在桌子旁边,如图所示,当火车突然加速时,小朋友看到小球相对火车的运动是( )
 光滑水平的桌面固定在向前做匀速直线运动的火车车厢内,桌上有相对火车静止的小球,一小朋友面朝火车前进方向坐在桌子旁边,如图所示,当火车突然加速时,小朋友看到小球相对火车的运动是( )
光滑水平的桌面固定在向前做匀速直线运动的火车车厢内,桌上有相对火车静止的小球,一小朋友面朝火车前进方向坐在桌子旁边,如图所示,当火车突然加速时,小朋友看到小球相对火车的运动是( )| A. | 向前滚动 | B. | 向右滚动 | C. | 向左滚动 | D. | 向后滚动 |
7.以8m/s的速度飞行的蜻蜓,在0.7s内停下来,则其加速度大小为( )
| A. | 0.09m/s2 | B. | 5.6m/s2 | C. | 9m/s2 | D. | 11.4m/s2 |

 如图所示,装置可绕竖直轴O′O转动,可视为质点的小球A与两细线连接后分别系
如图所示,装置可绕竖直轴O′O转动,可视为质点的小球A与两细线连接后分别系