题目内容
长L=0.5 m、质量可忽略的杆,其一端固定于O点,另一端连有质量m=2 kg的小球,它绕O点在竖直平面内做圆周运动.当通过最高点时,如图所示,求下列情况下,杆受到的力(计算出大小,并说明是拉力还是压力,g取10 m/s2):
(1)当v=1 m/s时,杆受到的力多大,是什么力?
(2)当v=4 m/s时,杆受到的力多大,是什么力?

【答案】
(1)16 N 支持力 (2)44 N 拉力
【解析】(1)当v=1 m/s时,小球所需向心力F1=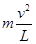 =
=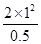 N=4 N<mg,所需向心力小于重力,小球有向轨道内侧运动的趋势,则杆对球为支持力,受力如图.
N=4 N<mg,所需向心力小于重力,小球有向轨道内侧运动的趋势,则杆对球为支持力,受力如图.

小球满足mg-N=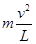 ,则
,则
N=mg-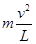 =2.0×10 N-
=2.0×10 N-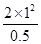 N=16 N
N=16 N
由牛顿第三定律可知,杆受到压力N′=16 N,方向竖直向下.

(2)当v=4
m/s时,小球所需向心力F2=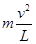 =
= N=64
N>mg.显然重力不能提供足够的向心力,则杆对球有一拉力,受力如图所示.
N=64
N>mg.显然重力不能提供足够的向心力,则杆对球有一拉力,受力如图所示.
小球满足mg+T=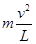 即
即
T=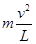 -mg=
-mg= N-2×10 N=44 N
N-2×10 N=44 N
由牛顿第三定律可知,小球对杆有一拉力,大小T′=44 N.
方向竖直向上.
思路分析:根据公式F向=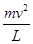 分析,当v=
分析,当v= 时,F向=
时,F向=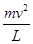 =mg,此时杆恰对小球无作用力,向心力只由其自身重力来提供,,当v由
=mg,此时杆恰对小球无作用力,向心力只由其自身重力来提供,,当v由 增大时,杆对球的力为拉力,且逐渐增大;当v由
增大时,杆对球的力为拉力,且逐渐增大;当v由 减小时,对球的力为支持力,
减小时,对球的力为支持力,
试题点评:本题考查了是小球在杆的作用下做圆周运动时,小球的速度变化导致小球对杆的作用力的变化,关键是找出临界点,即F向=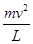 =mg,此时杆恰对小球无作用力,向心力只由其自身重力来提供,
=mg,此时杆恰对小球无作用力,向心力只由其自身重力来提供,

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目



