题目内容
如图是在光滑水平地面上有一辆平板小车，车上放着一个滑块，滑块和平板小车间有摩擦，滑块在水平恒力F作用下从车的一端拉到另一端．第一次拉滑块时将小车固定，第二次拉时小车没有固定．在这先后两次拉动木块的过程中，下列说法中正确的是（ ）分析：以地面为参考系，找出两次滑块位移，然后根据功的定义求解功，并根据功能关系判断动能增加量和内能增加量．
解答：解：A、滑动摩擦力与压力成正比，两次压力相等，都等于mg，动摩擦因素是一定的，故滑动摩擦力一定相等，故A正确；
B、第二次由于小车也会向右移动，故滑块的对地位移变大了，故拉力做的功变多了，故B错误；
C、根据动能定理，有：（F-f）x=
mv2；第二次由于小车也会向右移动，滑块的对地位移x变大了，故获得的动能也变大了，故C错误；
D、根据功能关系，系统增加的内能等于一对滑动摩擦力做的功，即：Q=f?△S；两次相对路程都等于小车的长度，故产生的内能相等，故D正确；
故选AD．
B、第二次由于小车也会向右移动，故滑块的对地位移变大了，故拉力做的功变多了，故B错误；
C、根据动能定理，有：（F-f）x=
| 1 |
| 2 |
D、根据功能关系，系统增加的内能等于一对滑动摩擦力做的功，即：Q=f?△S；两次相对路程都等于小车的长度，故产生的内能相等，故D正确；
故选AD．
点评：本题关键是明确功的定义和功能关系，要知道系统增加的内能等于一对滑动摩擦力做的功，即：Q=f?△S．
练习册系列答案
相关题目
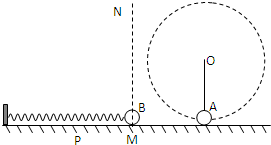如图所示，水平地面上方被竖直线MN分隔成两部分，M点左侧地面粗糙，与B球间的动摩擦因数为μ=0.5，右侧光滑．MN右侧空间有一范围足够大的匀强电场，在O点用长为R=5m的轻质绝缘细绳，拴一个质量mA=0.04kg，带电量为q=+2×10-4C的小球A，在竖直平面内以v=10m/s的速度做顺时针匀速圆周运动，小球A运动到最低点时与地面刚好不接触．处于原长的弹簧左端连在墙上，右端与不带电的小球B接触但不粘连，B球的质量mB=0.02kg，此时B球刚好位于M点．现用水平向左的推力将B球缓慢推至P点（弹簧仍在弹性限度内），MP之间的距离为L=10cm，推力所做的功是W=0.27J，当撤去推力后，B球沿地面向右滑动恰好能和A球在最低点处发生正碰，并瞬间成为一个整体C（A、B、C均可视为质点），速度大小变为5m/s，方向向左；碰撞前后电荷量保持不变，碰后瞬间立即把匀强电场的场强大小变为E=6×103N/C，电场方向不变，求：
（2006?西城区一模）如图所示，水平地面AB距离S=10m．BCD是半径为R=0.9m的光滑半圆轨道，O是圆心，DOB在同一竖直线上．一个质量m=1.0kg的物体静止在A点．现用F=10N的水平恒力作用在物体上，使物体从静止开始做匀加速直线运动．物体与水平地面间的动摩擦因数μ=0.5．当物体运动到B点时撤去F，以后物体沿BCD轨道运动，离开最高点D后落到地上的P点（图中未画出）．g取10m/s2．求：
如图所示，水平地面M点左侧粗糙，右侧光滑．整个空间有一场强大小E1=1×103N/C、方向竖直向下的匀强电场．质量mA=0.04kg的不带电小物块A用长为R=5m不可伸长的绝缘轻质细绳拴于O点，静止时与地面刚好接触．带正电的小物块B与左端固定在墙上的绝缘轻弹簧接触但不粘连，B的质量mB=0.02kg，带电量为q=+2×10-4 C，与M左侧地面间动摩擦因数μ=0.5．现用水平向左的推力将B由M点（弹簧原长处）缓慢推至P点（弹簧仍在弹性限度内），推力做功W=2.65J，MP之间的距离为L=50cm．撤去推力，B向右运动，随后与A发生正碰并瞬间成为一个整体C（A、B、C均可视为质点）．已知碰撞前后电荷量保持不变，碰后C的速度为碰前B速度的
（2009?丰台区一模）如图所示，水平地面上方被竖直线MN分隔成两部分，M点左侧地面粗糙，动摩擦因数为μ=0.5，右侧光滑．MN右侧空间有一范围足够大的匀强电场．在O点用长为R=5m的轻质绝缘细绳，拴一个质量mA=0.04kg，带电量为q=+2×10-4的小球A，在竖直平面内以v=10m/s的速度做顺时针匀速圆周运动，运动到最低点时与地面刚好不接触．处于原长的弹簧左端连在墙上，右端与不带电的小球B接触但不粘连，B球的质量mB=0.02kg，此时B球刚好位于M点．现用水平向左的推力将B球缓慢推至P点（弹簧仍在弹性限度内），MP之间的距离为L=10cm，推力所做的功是W=0.27J，当撤去推力后，B球沿地面右滑恰好能和A球在最低点处发生正碰，并瞬间成为一个整体C（A、B、C均可视为质点），碰后瞬间立即把匀强电场的场强大小变为E=6×103N/C，电场方向不变．（取g=10m/s2）求：