题目内容
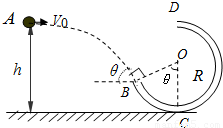
如图,竖直平面内有一光滑圆弧轨道,其半径为R=0.5m,平台与轨道的最高点等高,一质量m=lkg的小球从平台边缘的A处水平射出,恰能沿圆弧轨道上B点的切线方向进入轨道内侧,轨道半径OB与竖直线的夹角为53°,已知sin53°=0.8,cos53°=0,6,g取10m/s2.试求:(1)小球从平台上的A点射出时的速度大小v;
(2)小球沿轨道通过圆弧的最高点Q时对轨道的压力大小.
【答案】分析:(1)恰好从光滑圆弧PQ的P点的切线方向进入圆弧,说明到到P点的速度vP方向与水平方向的夹角为θ,这样可以求出初速度v;
(2)根据机械能守恒定律求得Q点速度,再运用牛顿第二定律和圆周运动知识求解.
解答:解:(1)小球从A到P的高度差h=R(1+cos53°)①
小球做平抛运动有 h=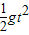 ②
②
则小球在P点的竖直分速度vy=gt③
把小球在P点的速度分解可得vtan53°=vy ④
由①②③④解得:小球平抛初速度v=3m/s
(2)小球从A到达Q时,根据机械能守恒定律可知vQ=v=3m/s
在Q点根据向心力公式得:
m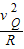 =N+mg
=N+mg
解得;N=m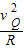 -mg=14.4-8=6.4N
-mg=14.4-8=6.4N
根据牛顿第三定律得:小球沿轨道通过圆弧的最高点Q时对轨道的压力N′=N=6.4N
答:(1)小球从平台上的A点射出时的速度大小为3m/s;
(2)小球沿轨道通过圆弧的最高点Q时对轨道的压力大小为6.4N
点评:恰能无碰撞地沿圆弧切线从B点进入光滑竖直圆弧轨道,这是解这道题的关键,理解了这句话就可以求得小球的末速度,本题很好的把平抛运动和圆周运动结合在一起运用机械能守恒解决,能够很好的考查学生的能力,较难.
(2)根据机械能守恒定律求得Q点速度,再运用牛顿第二定律和圆周运动知识求解.
解答:解:(1)小球从A到P的高度差h=R(1+cos53°)①
小球做平抛运动有 h=
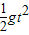 ②
②则小球在P点的竖直分速度vy=gt③
把小球在P点的速度分解可得vtan53°=vy ④
由①②③④解得:小球平抛初速度v=3m/s
(2)小球从A到达Q时,根据机械能守恒定律可知vQ=v=3m/s
在Q点根据向心力公式得:
m
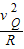 =N+mg
=N+mg解得;N=m
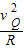 -mg=14.4-8=6.4N
-mg=14.4-8=6.4N根据牛顿第三定律得:小球沿轨道通过圆弧的最高点Q时对轨道的压力N′=N=6.4N
答:(1)小球从平台上的A点射出时的速度大小为3m/s;
(2)小球沿轨道通过圆弧的最高点Q时对轨道的压力大小为6.4N
点评:恰能无碰撞地沿圆弧切线从B点进入光滑竖直圆弧轨道,这是解这道题的关键,理解了这句话就可以求得小球的末速度,本题很好的把平抛运动和圆周运动结合在一起运用机械能守恒解决,能够很好的考查学生的能力,较难.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 如图,竖直平面内有一光滑圆弧轨道,其半径为R=0.5m,平台与轨道的最高点等高,一质量m=lkg的小球从平台边缘的A处水平射出,恰能沿圆弧轨道上B点的切线方向进入轨道内侧,轨道半径OB与竖直线的夹角为53°,已知sin53°=0.8,cos53°=0,6,g取10m/s2.试求:
如图,竖直平面内有一光滑圆弧轨道,其半径为R=0.5m,平台与轨道的最高点等高,一质量m=lkg的小球从平台边缘的A处水平射出,恰能沿圆弧轨道上B点的切线方向进入轨道内侧,轨道半径OB与竖直线的夹角为53°,已知sin53°=0.8,cos53°=0,6,g取10m/s2.试求: (1)对于一定质量的理想气体,下列说法正确的是
(1)对于一定质量的理想气体,下列说法正确的是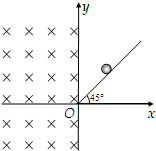 (2011?株洲二模)如图,竖直平面内有一直角坐标系xOy,在x≥0的区域内有一倾角为45°的绝缘光滑斜面,斜面末端O处用一极小的平滑曲面连接,恰能使斜面末端水平.在x≤0的广泛区域内存在正交的匀强磁场和匀强电场,磁场垂直于纸面向里,磁感应强度大小为B;电场沿竖直方向,场强大小为E.电荷量为-q的带电小球从绝缘光滑斜面上某点由静止开始下滑,小球经斜面末端O点进入电场和磁场,之后沿圆周运动,垂直于y轴离开电场和磁场,最后垂直打到斜面上.
(2011?株洲二模)如图,竖直平面内有一直角坐标系xOy,在x≥0的区域内有一倾角为45°的绝缘光滑斜面,斜面末端O处用一极小的平滑曲面连接,恰能使斜面末端水平.在x≤0的广泛区域内存在正交的匀强磁场和匀强电场,磁场垂直于纸面向里,磁感应强度大小为B;电场沿竖直方向,场强大小为E.电荷量为-q的带电小球从绝缘光滑斜面上某点由静止开始下滑,小球经斜面末端O点进入电场和磁场,之后沿圆周运动,垂直于y轴离开电场和磁场,最后垂直打到斜面上. 如图,竖直平面内有一直角形内径相同的 细玻璃管,A端封闭,C端开口,AB=BC=l0,且此时A、C端等高.管内水银总长度为l0,玻璃管AB内封闭有长为
如图,竖直平面内有一直角形内径相同的 细玻璃管,A端封闭,C端开口,AB=BC=l0,且此时A、C端等高.管内水银总长度为l0,玻璃管AB内封闭有长为 ,且此时A、C端等高。平街时,管内水银总长度为
,且此时A、C端等高。平街时,管内水银总长度为