题目内容
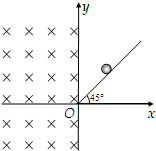 (2011?株洲二模)如图,竖直平面内有一直角坐标系xOy,在x≥0的区域内有一倾角为45°的绝缘光滑斜面,斜面末端O处用一极小的平滑曲面连接,恰能使斜面末端水平.在x≤0的广泛区域内存在正交的匀强磁场和匀强电场,磁场垂直于纸面向里,磁感应强度大小为B;电场沿竖直方向,场强大小为E.电荷量为-q的带电小球从绝缘光滑斜面上某点由静止开始下滑,小球经斜面末端O点进入电场和磁场,之后沿圆周运动,垂直于y轴离开电场和磁场,最后垂直打到斜面上.
(2011?株洲二模)如图,竖直平面内有一直角坐标系xOy,在x≥0的区域内有一倾角为45°的绝缘光滑斜面,斜面末端O处用一极小的平滑曲面连接,恰能使斜面末端水平.在x≤0的广泛区域内存在正交的匀强磁场和匀强电场,磁场垂直于纸面向里,磁感应强度大小为B;电场沿竖直方向,场强大小为E.电荷量为-q的带电小球从绝缘光滑斜面上某点由静止开始下滑,小球经斜面末端O点进入电场和磁场,之后沿圆周运动,垂直于y轴离开电场和磁场,最后垂直打到斜面上.求:
(1)小球从开始运动到垂直打到斜面上所用时间.
(2)小球开始下滑的初始位置坐标.
分析:(1)画出小球运动的轨迹,小球经过三个运动过程:1、由静止开始匀加速运动到斜面末端,由速度公式v0=gsin45°t1求出时间的表达式;2、在左侧复合场中做匀速圆周运动,半径为r=
,时间t2=
T=
;3、y轴离开电场和磁场后做平抛运动,垂直落到斜面时,v0=vytan45°=gt3,竖直方向位移为 2r-y2=
g
,y2=x2=v0t3,联立解得各段时间,即可求出总时间.
(2)小球初始位置到斜面末端的距离为 l=
gsin45°
,由上求得t1,即可求出位置的坐标.
| mv0 |
| qB |
| 1 |
| 2 |
| πm |
| qB |
| 1 |
| 2 |
| t | 2 3 |
(2)小球初始位置到斜面末端的距离为 l=
| 1 |
| 2 |
| t | 2 1 |
解答: 解:(1)小球运动的轨迹如图.初始位置(x1,y1),再次回到斜面的落点位置(x2,y2),小球经时间t1运动到末端的速度为v0,则
解:(1)小球运动的轨迹如图.初始位置(x1,y1),再次回到斜面的落点位置(x2,y2),小球经时间t1运动到末端的速度为v0,则
t1=
①
小球在复合场中做匀速圆周运动,则有 mg=qE ②
轨道半径为 r=
③
运动时间为 t2=
T=
④
小球离开电磁场后做平抛运动,经时间t3垂直落到斜面时
v0=vytan45°=gt3 ⑤
2r-y2=
g
⑥
y2=x2=v0t3,⑦
由②③⑤⑥⑦得,t3=
⑧v0=
⑨
由②④得,t2=
⑩
由①⑨得,t1=
故小球从开始运动到垂直打到斜面上所用时间为t=t1+t2+t3=(
+π)
.
(2)小球初始位置到斜面末端的距离为 l=
gsin45°
=
故 x1=y1=lsin45°=
答:
(1)小球从开始运动到垂直打到斜面上所用时间为(
+π)
..
(2)小球开始下滑的初始位置坐标(
,
).
 解:(1)小球运动的轨迹如图.初始位置(x1,y1),再次回到斜面的落点位置(x2,y2),小球经时间t1运动到末端的速度为v0,则
解:(1)小球运动的轨迹如图.初始位置(x1,y1),再次回到斜面的落点位置(x2,y2),小球经时间t1运动到末端的速度为v0,则t1=
| v0 |
| gsin45° |
小球在复合场中做匀速圆周运动,则有 mg=qE ②
轨道半径为 r=
| mv0 |
| qB |
运动时间为 t2=
| 1 |
| 2 |
| πm |
| qB |
小球离开电磁场后做平抛运动,经时间t3垂直落到斜面时
v0=vytan45°=gt3 ⑤
2r-y2=
| 1 |
| 2 |
| t | 2 3 |
y2=x2=v0t3,⑦
由②③⑤⑥⑦得,t3=
| 4E |
| 3gB |
| 4E |
| 3B |
由②④得,t2=
| πE |
| gB |
由①⑨得,t1=
4
| ||
| 3gB |
故小球从开始运动到垂直打到斜面上所用时间为t=t1+t2+t3=(
4(
| ||
| 3 |
| E |
| gB |
(2)小球初始位置到斜面末端的距离为 l=
| 1 |
| 2 |
| t | 2 1 |
8
| ||
| 9gB2 |
故 x1=y1=lsin45°=
| 8E2 |
| 9gB2 |
答:
(1)小球从开始运动到垂直打到斜面上所用时间为(
4(
| ||
| 3 |
| E |
| gB |
(2)小球开始下滑的初始位置坐标(
| 8E2 |
| 9gB2 |
| 8E2 |
| 9gB2 |
点评:本题的运动过程比较复杂,既要单独分析各段过程的运动情况,又抓住各过程之间的联系,这是解题的关键所在.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2011?株洲二模)如图所示,L1、L2为二个相同的灯泡,R0为定值电阻,定值电阻的阻值与灯泡电阻相同.在变阻器R的滑片P向上移动过程中( )
(2011?株洲二模)如图所示,L1、L2为二个相同的灯泡,R0为定值电阻,定值电阻的阻值与灯泡电阻相同.在变阻器R的滑片P向上移动过程中( ) (2011?株洲二模)如图所示,质量为m的铁球置于一“V”形槽内(A、B两侧对称),“V”形槽只在水平方向做直线运动,且球与槽无相对运动.设球对A、B两侧的压力分别为NA、NB,忽略一切摩擦,以下说法中正确的是( )
(2011?株洲二模)如图所示,质量为m的铁球置于一“V”形槽内(A、B两侧对称),“V”形槽只在水平方向做直线运动,且球与槽无相对运动.设球对A、B两侧的压力分别为NA、NB,忽略一切摩擦,以下说法中正确的是( ) (2011?株洲二模)一木块放在水平地面上,在力F=2N作用下向右运动,水平地面AB段光滑,BC段粗糙,木块从A点运动到C点的v-t图如图所示,取 g=10m/s2,则( )
(2011?株洲二模)一木块放在水平地面上,在力F=2N作用下向右运动,水平地面AB段光滑,BC段粗糙,木块从A点运动到C点的v-t图如图所示,取 g=10m/s2,则( )