题目内容
2.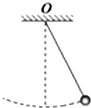 如图所示,质量为1kg的小球用细绳悬挂于O点,将小球拉离竖直位置释放后,到达最低点时的速度为2m/s,已知球心到悬点的距离为1m,重力加速度g=10m/s2,求小球在最低点时对绳的拉力的大小.
如图所示,质量为1kg的小球用细绳悬挂于O点,将小球拉离竖直位置释放后,到达最低点时的速度为2m/s,已知球心到悬点的距离为1m,重力加速度g=10m/s2,求小球在最低点时对绳的拉力的大小.
分析 小球经过最低点时,由重力与绳子拉力的合力提供向心力,根据牛顿第二定律列方程求解.
解答 解:小球经过最低点时,由重力与绳子拉力的合力提供向心力,根据牛顿第二定律得:
T-mg=m$\frac{{v}^{2}}{L}$得,
T=m(g+$\frac{{v}^{2}}{L}$)=1×(10+$\frac{4}{1}$)N=14N
根据牛顿第三定律可知,小球在最低点时对绳的拉力的大小为14N.
答:在最低点绳对小球的拉力为14N.
点评 对于圆周运动动力学问题,关键通过分析物体的受力情况,确定向心力的来源,实质是牛顿第二定律的特殊应用.

练习册系列答案
相关题目
12.两个电流随时间的变化关系如图甲、乙所示,把它们通人相同的电阻中,则在1s内两电阻消耗的电功之比Wa:Wb等于( )


| A. | 1:$\sqrt{2}$ | B. | 1:2 | C. | 1:4 | D. | 1:1 |
7. 如图所示,质量相等的A、B两物块放在匀速转动的水平圆盘上,随圆盘一起做匀速圆周运动,则下列说法中正确的是( )
如图所示,质量相等的A、B两物块放在匀速转动的水平圆盘上,随圆盘一起做匀速圆周运动,则下列说法中正确的是( )
 如图所示,质量相等的A、B两物块放在匀速转动的水平圆盘上,随圆盘一起做匀速圆周运动,则下列说法中正确的是( )
如图所示,质量相等的A、B两物块放在匀速转动的水平圆盘上,随圆盘一起做匀速圆周运动,则下列说法中正确的是( )| A. | 它们所受的摩擦力fA>fB | |
| B. | 它们的线速度VA<VB | |
| C. | 它们的角速度ωA>ωB | |
| D. | 若圆盘转速增大,A、B同时相对圆盘滑动 |
7.在“验证力的平行四边形定则”中,用两只弹簧秤分别勾住细绳套,互成角度地拉橡皮条,使它伸长到某一位置O,此时,必须记录的是( )
| A. | O点的位置 | B. | 橡皮条固定端位置 | ||
| C. | 两只弹簧秤的读数 | D. | 两条细绳套之间的夹角 | ||
| E. | 两条细绳套的方向 | F. | 橡皮条的伸长长度 |
 如图所示,高为h=0.5m的木块放在离地高为H=4.5m的平台边缘上,质量为m2=0.5kg的小球2放在木块上,质量为m1=1kg的小球1与小球2等高,现把小球1拉到离平台高为h1=0.55m的A处后由静止释放,到最低点时与球2正碰,碰后球2落在地面上的C处,C与平台边缘的水平距离为L=1m,g=10m/s2.求:
如图所示,高为h=0.5m的木块放在离地高为H=4.5m的平台边缘上,质量为m2=0.5kg的小球2放在木块上,质量为m1=1kg的小球1与小球2等高,现把小球1拉到离平台高为h1=0.55m的A处后由静止释放,到最低点时与球2正碰,碰后球2落在地面上的C处,C与平台边缘的水平距离为L=1m,g=10m/s2.求: 如图所示,倾角为α的斜面体A置于粗糙水平面上,物体B置于斜面上,已知A.B的质量分别为M,m.它们之间的动摩擦因数为μ=tanα,现给一平行于斜面向下的恒定的推力F,使B沿斜面向下运动,A始终处于静止状态,水平面对A的摩擦力怎样?
如图所示,倾角为α的斜面体A置于粗糙水平面上,物体B置于斜面上,已知A.B的质量分别为M,m.它们之间的动摩擦因数为μ=tanα,现给一平行于斜面向下的恒定的推力F,使B沿斜面向下运动,A始终处于静止状态,水平面对A的摩擦力怎样? 如图所示为一横波图象,此时质点A的速度沿y轴正向,振动频率是0.5Hz,则此波向右方向传播,图中质点B经过5.5s通过的路程是1.1cm,偏离平衡位置的位移是0cm.
如图所示为一横波图象,此时质点A的速度沿y轴正向,振动频率是0.5Hz,则此波向右方向传播,图中质点B经过5.5s通过的路程是1.1cm,偏离平衡位置的位移是0cm.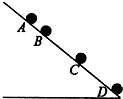 从斜面上某一位置每隔0.1s释放一些相同的小球,在连续释放几个小球之后,对斜面上运动的小球摄下照片如图所示,测得AB=15cm,BC=20cm.试求:
从斜面上某一位置每隔0.1s释放一些相同的小球,在连续释放几个小球之后,对斜面上运动的小球摄下照片如图所示,测得AB=15cm,BC=20cm.试求: