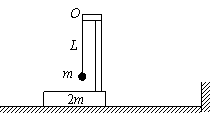
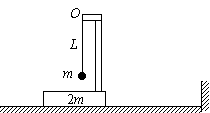
题目内容
如图所示,质量不计且足够长的倒L型支架下端固定在质量为2m的木板上,在其上端O处系一长为L的轻绳,绳的下端系一质量为m的小球,小球可视为质点.整个装置在光滑的水平面上以速度v向右作匀速直线运动,水平面的右端为一矮墙壁.①若木板与墙壁相碰后即与墙壁粘合在一起,试求碰后小球上升至最高点时绳中的张力大小(小球在运动过程中不与支架相碰).
②若木板与墙壁相碰后以原速率反弹,要使绳的最大偏角不超过90°,则绳长L应满足什么条件?
③在满足第2问的条件下,则当小球运动至最低点时,木板对地的压力是多大?

【答案】分析:(1)木板与墙壁相碰立即与墙壁粘合在一起,小球以速度v向右做圆周运动,速度v在不同的范围内小球的运动情况不同,分情况讨论.
(2)绳的偏角最大时,球与木板的共同速度为υ,根据动量守恒求得共同速度,再根据机械能守恒求得绳长.
(3)当小球运动至最低点时,根据系统水平方向动量守恒和机械能守恒,列式求出小球和木板的速度.在最低点时,由重力和细绳的拉力的合力提供向心力,根据牛顿第二定律细绳的拉力,再对木板研究,即可求得地对板的支持力,由牛顿第三定律求出木板对地的压力.
解答:解:①当v≤ 时,设球上升到最高点时绳与竖直方向的夹角为θ.
时,设球上升到最高点时绳与竖直方向的夹角为θ.
对小球向上摆动的过程有:mgL(1-cosθ)=
小球在最高点时有:T=mgcosθ
解得张力:T=mg-
当 <V0<
<V0< 时,绳松弛后小球作斜上抛运动,故张力T=0
时,绳松弛后小球作斜上抛运动,故张力T=0
当 时,设球运动到最高点时速度为v.
时,设球运动到最高点时速度为v.
对小球从最低点到最高点的过程有: -
- =mg?2L
=mg?2L
小球在最高点时有:T+mg=m
解得张力:T=m -5mg
-5mg
②若绳长为L时,碰后绳的最大偏角为90,球与木板的共同速度为v
据动量守恒得:2mv-mv=3mv
据机械能守恒得:mgL= ?3m
?3m -
-
解得:
所以当L满足L≥ 时,绳的偏角不超过90
时,绳的偏角不超过90
③设小球运动到最低点时,小球、木板的速度分别为v1、v2,据动量、能量守恒得
2mυ-mυ=mυ1+mv2
据机械能守恒得:
 ?3m
?3m =
= m
m +
+
解得:v1=-v(?-?表示小球向右通过最低点),v2=v
v1= ,
, (?-?表示木板向右运动)
(?-?表示木板向右运动)
不论小球向左还是向右通过最低点,球相对于板的速度v’均为2v,即:v′=2v
对最低点的小球有:T-mg=m
对木板有:N=T+2mg
据牛顿第三定律得:板对地压力大小N′=N
解得:N′=3mg+
答:
①若木板与墙壁相碰后即与墙壁粘合在一起,碰后小球上升至最高点时绳中的张力大小为m -5mg.
-5mg.
②若木板与墙壁相碰后以原速率反弹,要使绳的最大偏角不超过90°,则绳长L应满足L≥ .
.
③在满足第2问的条件下,则当小球运动至最低点时,木板对地的压力是3mg+ .
.
点评:本题中细绳带小球在竖直面内做圆周运动,小球需要向心力,根据小球获得速度的大小判断小球的运动情况.该题是把动量守恒和机械能守恒结合得综合应用.
(2)绳的偏角最大时,球与木板的共同速度为υ,根据动量守恒求得共同速度,再根据机械能守恒求得绳长.
(3)当小球运动至最低点时,根据系统水平方向动量守恒和机械能守恒,列式求出小球和木板的速度.在最低点时,由重力和细绳的拉力的合力提供向心力,根据牛顿第二定律细绳的拉力,再对木板研究,即可求得地对板的支持力,由牛顿第三定律求出木板对地的压力.
解答:解:①当v≤
 时,设球上升到最高点时绳与竖直方向的夹角为θ.
时,设球上升到最高点时绳与竖直方向的夹角为θ.对小球向上摆动的过程有:mgL(1-cosθ)=

小球在最高点时有:T=mgcosθ
解得张力:T=mg-

当
 <V0<
<V0< 时,绳松弛后小球作斜上抛运动,故张力T=0
时,绳松弛后小球作斜上抛运动,故张力T=0 当
 时,设球运动到最高点时速度为v.
时,设球运动到最高点时速度为v.对小球从最低点到最高点的过程有:
 -
- =mg?2L
=mg?2L 小球在最高点时有:T+mg=m

解得张力:T=m
 -5mg
-5mg ②若绳长为L时,碰后绳的最大偏角为90,球与木板的共同速度为v
据动量守恒得:2mv-mv=3mv
据机械能守恒得:mgL=
 ?3m
?3m -
-
解得:

所以当L满足L≥
 时,绳的偏角不超过90
时,绳的偏角不超过90 ③设小球运动到最低点时,小球、木板的速度分别为v1、v2,据动量、能量守恒得
2mυ-mυ=mυ1+mv2
据机械能守恒得:
 ?3m
?3m =
= m
m +
+
解得:v1=-v(?-?表示小球向右通过最低点),v2=v
v1=
 ,
, (?-?表示木板向右运动)
(?-?表示木板向右运动) 不论小球向左还是向右通过最低点,球相对于板的速度v’均为2v,即:v′=2v
对最低点的小球有:T-mg=m

对木板有:N=T+2mg
据牛顿第三定律得:板对地压力大小N′=N
解得:N′=3mg+

答:
①若木板与墙壁相碰后即与墙壁粘合在一起,碰后小球上升至最高点时绳中的张力大小为m
 -5mg.
-5mg. ②若木板与墙壁相碰后以原速率反弹,要使绳的最大偏角不超过90°,则绳长L应满足L≥
 .
.③在满足第2问的条件下,则当小球运动至最低点时,木板对地的压力是3mg+
 .
.点评:本题中细绳带小球在竖直面内做圆周运动,小球需要向心力,根据小球获得速度的大小判断小球的运动情况.该题是把动量守恒和机械能守恒结合得综合应用.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
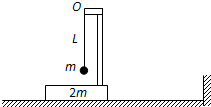 如图所示,质量不计且足够长的倒L型支架下端固定在质量为2m的木板上,在其上端O处系一长为L的轻绳,绳的下端系一质量为m的小球,小球可视为质点.整个装置在光滑的水平面上以速度v0向右做匀速直线运动,水平面的右端为一矮墙.(重力加速度为g)
如图所示,质量不计且足够长的倒L型支架下端固定在质量为2m的木板上,在其上端O处系一长为L的轻绳,绳的下端系一质量为m的小球,小球可视为质点.整个装置在光滑的水平面上以速度v0向右做匀速直线运动,水平面的右端为一矮墙.(重力加速度为g)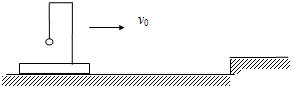 如图所示,质量不计且足够长的倒L型支架下端固定在质量为2m的木板上,在其上端O处系一长为L的轻绳,绳的下端系一质量为m的小球,小球可视为质点.整个装置在光滑的水平面上以速度v0向右作匀速直线运动,水平面的右端为一矮墙壁.
如图所示,质量不计且足够长的倒L型支架下端固定在质量为2m的木板上,在其上端O处系一长为L的轻绳,绳的下端系一质量为m的小球,小球可视为质点.整个装置在光滑的水平面上以速度v0向右作匀速直线运动,水平面的右端为一矮墙壁.