题目内容
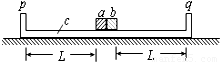
静止放置在水平面上的长木板c的两端装有固定的竖直挡板p、q,两个小滑块a、b放置在长木板上,与两端挡板的距离都为L,如图所示.a、c的质量都为m,b的质量为3m.a、b之间夹有少量的火药,火药点燃后在很短时间内将两个滑块从静止分开,两个滑块获得的总动能为E,设一切摩擦力均可忽略不计,滑块碰到挡板时立刻与挡板粘合在一起.求:(1)a、b分开后滑块a、b的速度.
(2)滑块a碰到挡板p时,b与挡板q之间的距离.
(3)长木板在水平面上发生的总位移.
【答案】分析:(1)ab分开后同时满足动量守恒,再根据滑块的总动能为E求解即可;
(2)由(1)求出的两速度,根据滑块做匀速直线运动,根据位移关系求解a碰到挡板P时,b的位移,抓住运动时间相同;
(3)a与挡板碰撞后,根据动量守恒长木板获得速度,当b与挡板碰撞后长木板静止,根据位移关系确定长木板的运动位移.
解答:解:(1)设a、b分开后速度大小各为v1、v2.
依题意得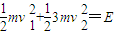
取水平向左的方向为正方向,根据动量守恒定律得0=mv1-3mv2
解得a、b分开后滑块a、b的速度分别是:
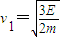 (方向向左)
(方向向左)
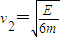 (方向向右)
(方向向右)
(2)设a经过时间t1碰到挡板p,则
a的位移为L=v1t1
b的位移为sb=v2t1
解得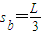
此时b与挡板q之间的距离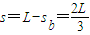
(3)设a碰撞挡板p后共同速度为v3,根据动量守恒定律得mv1=2mv3
设再经过时间t2时b碰到挡板p,则
c的位移为sc=v3t2
b的位移为s'b=v2t2
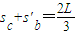
解得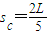
b与挡板q碰撞,根据动量守恒定律得2mv3-3mv2=5mv
可得碰后速度v=0,整体停下.
因此长木板在水平面上发生的总位移为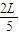 .
.
点评:火药点燃后,抓住动量守恒和动能一定这是解决两滑块速度的入手,由于忽略一切摩擦,ab运动过程中长木板保持静止,每个滑块与挡板碰撞过程中都满足动量守恒是解决本题的关键.
(2)由(1)求出的两速度,根据滑块做匀速直线运动,根据位移关系求解a碰到挡板P时,b的位移,抓住运动时间相同;
(3)a与挡板碰撞后,根据动量守恒长木板获得速度,当b与挡板碰撞后长木板静止,根据位移关系确定长木板的运动位移.
解答:解:(1)设a、b分开后速度大小各为v1、v2.
依题意得
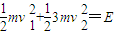
取水平向左的方向为正方向,根据动量守恒定律得0=mv1-3mv2
解得a、b分开后滑块a、b的速度分别是:
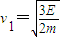 (方向向左)
(方向向左) 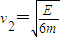 (方向向右)
(方向向右) (2)设a经过时间t1碰到挡板p,则
a的位移为L=v1t1
b的位移为sb=v2t1
解得
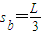
此时b与挡板q之间的距离
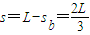
(3)设a碰撞挡板p后共同速度为v3,根据动量守恒定律得mv1=2mv3
设再经过时间t2时b碰到挡板p,则
c的位移为sc=v3t2
b的位移为s'b=v2t2
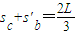
解得
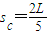
b与挡板q碰撞,根据动量守恒定律得2mv3-3mv2=5mv
可得碰后速度v=0,整体停下.
因此长木板在水平面上发生的总位移为
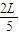 .
.点评:火药点燃后,抓住动量守恒和动能一定这是解决两滑块速度的入手,由于忽略一切摩擦,ab运动过程中长木板保持静止,每个滑块与挡板碰撞过程中都满足动量守恒是解决本题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
 (2013?重庆模拟)如题所示,质量为m的物块甲置于竖直放置在水平面上的轻弹簧上处于静止状态.若突然将质量为2m的物块乙无初速度地放在物块甲上,则在物块乙放在物块甲后瞬间,物块甲、乙的加速度分别为
(2013?重庆模拟)如题所示,质量为m的物块甲置于竖直放置在水平面上的轻弹簧上处于静止状态.若突然将质量为2m的物块乙无初速度地放在物块甲上,则在物块乙放在物块甲后瞬间,物块甲、乙的加速度分别为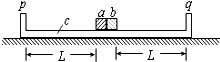 (2008?汕头二模)静止放置在水平面上的长木板c的两端装有固定的竖直挡板p、q,两个小滑块a、b放置在长木板上,与两端挡板的距离都为L,如图所示.a、c的质量都为m,b的质量为3m.a、b之间夹有少量的火药,火药点燃后在很短时间内将两个滑块从静止分开,两个滑块获得的总动能为E0,设一切摩擦力均可忽略不计,滑块碰到挡板时立刻与挡板粘合在一起.求:
(2008?汕头二模)静止放置在水平面上的长木板c的两端装有固定的竖直挡板p、q,两个小滑块a、b放置在长木板上,与两端挡板的距离都为L,如图所示.a、c的质量都为m,b的质量为3m.a、b之间夹有少量的火药,火药点燃后在很短时间内将两个滑块从静止分开,两个滑块获得的总动能为E0,设一切摩擦力均可忽略不计,滑块碰到挡板时立刻与挡板粘合在一起.求: 如图所示,质量为m1的物体甲通过三段轻绳悬挂,三段轻绳的结点为O.轻绳OB水平且B端与放置在水平面上的质量为m2的物体乙相连,轻绳OA与竖直方向的夹角θ=370,物体甲、乙均处于静止状态.(已知:sin37°=0.6,cos37°=0.8,设最大静摩擦力等于滑动摩擦力)求:
如图所示,质量为m1的物体甲通过三段轻绳悬挂,三段轻绳的结点为O.轻绳OB水平且B端与放置在水平面上的质量为m2的物体乙相连,轻绳OA与竖直方向的夹角θ=370,物体甲、乙均处于静止状态.(已知:sin37°=0.6,cos37°=0.8,设最大静摩擦力等于滑动摩擦力)求: