题目内容
电子的质量为m，电量大小为e，以速率V射入匀强电场中，V的方向和场强E的方向相同，设电子刚进入场区时电势能为零，则电子能进入场区最大深度为
，当电子进入场区深度为
时，其动能和电势能相等．
| mv02 |
| 2eE |
| mv02 |
| 2eE |
| mv02 |
| 4eE |
| mv02 |
| 4eE |
分析：要使电子的动能和电势能相等，电场力必须做负功，电子做匀减速运动，根据能量守恒求出此时电子的动能，再由动能定理求解电子进入电场的距离．
解答：解：
①电子进入场区最大深度时，动能全部转化为电势能，设最大深度为d，由动能定理可得：
-eEd=0-
mv02
解得：
d=
；
②由题意分析可知，电场力必须做负功，电子应做电子做匀减速运动，根据能量守恒得知：电子的动能与电势能相等时，其动能为初动能的一半，即为
mv02，
根据动能定理得：
-eEs=
mv02-
mv02
解得：
s=
；
故答案为：
；
．
①电子进入场区最大深度时，动能全部转化为电势能，设最大深度为d，由动能定理可得：
-eEd=0-
| 1 |
| 2 |
解得：
d=
| mv02 |
| 2eE |
②由题意分析可知，电场力必须做负功，电子应做电子做匀减速运动，根据能量守恒得知：电子的动能与电势能相等时，其动能为初动能的一半，即为
| 1 |
| 4 |
根据动能定理得：
-eEs=
| 1 |
| 4 |
| 1 |
| 2 |
解得：
s=
| mv02 |
| 4eE |
故答案为：
| mv02 |
| 2eE |
| mv02 |
| 4eE |
点评：本题的解题关键是分析电子的运动情况，运用动能定理求解，训练重点是动能定理的应用．
练习册系列答案
相关题目
如图为一示波管中的水平偏转极板，已知极板的长度为L，两板距离为d，所加偏转电压为U，且下板带正电；若一束电子以初速v0沿极板的中线进入偏转电场，最终电子从P点飞出．设电子的质量为m，电量为e，不计电子的重力．试求
保这些电子都不会从平行板的右侧穿出：
如图所示为电视机中显像管的原理示意图，电子枪中的灯丝因加热而逸出电子，这些电子再经加速电场加速后，从O点进入由磁偏转线圈产生的圆形匀强磁场区域中，经过偏转磁场后打到荧光屏MN上，使荧光屏发出荧光形成图象．磁场方向垂直于圆面，磁场区域的中心为O′，半径为r．当不加磁场时，电子束将通过O′点打到荧光屏的中心Q点．已知电子的质量为m，电量为e，加速电压为U，磁场区域的最右端到荧光屏的距离为9r．不计从灯丝逸出的电子的初速度和电子之间的相互作用．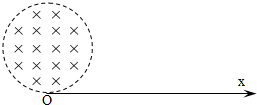
真空中有一半径为r的圆柱形匀强磁场区域，磁场方向垂直于纸面向里，ox为磁场边界上的切线，如图所示．从o点在纸面内向各个方向发射速率均为v0的带负电的粒子，设带电粒子间相互作用可忽略，且此种带负电的粒子在磁场中的偏转半径也是r．