题目内容
6. 如图所示,轨道ABCD的AB段为一半径R=0.2m的光滑$\frac{1}{4}$圆形轨道,BC段为高为h=5m的竖直轨道,CD段为水平轨道.一质量为0.1kg的小球由A点从静止开始下滑到B点时速度的大小为2m/s,离开B点做平抛运动(g取10m/s2),求:
如图所示,轨道ABCD的AB段为一半径R=0.2m的光滑$\frac{1}{4}$圆形轨道,BC段为高为h=5m的竖直轨道,CD段为水平轨道.一质量为0.1kg的小球由A点从静止开始下滑到B点时速度的大小为2m/s,离开B点做平抛运动(g取10m/s2),求:(1)小球到达B点时对圆形轨道的压力大小?
(2)小球离开B点后,在CD轨道上的落地点到B的距离.
分析 ①小球在B点时,由重力和轨道的支持力的合力提供向心力,由向心力的公式可以求得小球受到的支持力的大小,在根据牛顿第三定律可以知道对圆形轨道的压力大小.
②小球离开B点后做平抛运动,根据平抛运动的规律可以求得水平距离
解答 解:(1)小球达B受重力G和向上的弹力F作用,由牛顿第二定律知:
F-mg=$\frac{m{V}^{2}}{R}$
解得:F=3N
由牛顿第三定律知球对圆形轨道的压力大小为3N,方向竖直向下.
(2)设小球离开B点做平抛运动的时间为t1,落地点到C点距离为s,有:h=$\frac{1}{2}$gt12
得:t1=$\sqrt{\frac{2×5}{10}}$s=1 s
s=vBt1=2×1 m=2 m
小球离开B点后,在CD轨道上的落地点到B的距离为:
X=$\sqrt{{S}^{2}+{h}^{2}}$=$\sqrt{29}m/s$
答:(1)小球到达B点时对圆形轨道的压力大小3N
(2)小球离开B点后,在CD轨道上的落地点到B的距离$\sqrt{29}m/s$
点评 本题考查了圆周运动和平抛运动的规律,平抛运动可以分解为在水平方向上的匀速直线运动,和竖直方向上的自由落体运动来求解

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
17.在太阳系中有一颗行星的半径为R,若在该星球表面以初速度V0竖直上抛出一物体,则该物体上升的最大高度为H.已知该物体所受的其他力与行星对它的万有引力相比较可忽略不计,万有引力常量为G.则根据这些条件,可以求出的物理量是( )
| A. | 该行星的自转周期 | B. | 该行星的密度 | ||
| C. | 该星球的第一宇宙速度 | D. | 绕该行星运行的卫星的最小周期 |
1.(多选)关于万有引力,下列说法不正确的是( )
| A. | 牛顿正式提出了万有引力定律并利用扭秤测出了引力常量 | |
| B. | 测量引力常量的扭秤实验涉及的物理思想方法是微小量放大法 | |
| C. | 根据万有引力公式可知,假设地球球心有一物体,则它和地球之间的万有引力会趋于无穷大 | |
| D. | 德国天文学家开普勒提出开普勒三大定律 |
9. 火车在倾斜的轨道上转弯如图所示,弯道的倾角为θ,半径为r,则火车在转弯时车轮与铁轨无侧向压力的速率是(设转弯半径水平)( )
火车在倾斜的轨道上转弯如图所示,弯道的倾角为θ,半径为r,则火车在转弯时车轮与铁轨无侧向压力的速率是(设转弯半径水平)( )
 火车在倾斜的轨道上转弯如图所示,弯道的倾角为θ,半径为r,则火车在转弯时车轮与铁轨无侧向压力的速率是(设转弯半径水平)( )
火车在倾斜的轨道上转弯如图所示,弯道的倾角为θ,半径为r,则火车在转弯时车轮与铁轨无侧向压力的速率是(设转弯半径水平)( )| A. | $\sqrt{grsinθ}$ | B. | $\sqrt{grcosθ}$ | C. | $\sqrt{grtanθ}$ | D. | $\sqrt{\frac{gr}{tanθ}}$ |
12.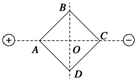 如图所示,在等量异种电荷形成的电场中,画一正方形ABCD,对角线AC与两点电荷连线重合,两对角线交点O恰为电荷连线的中点.下列说法中正确的是( )
如图所示,在等量异种电荷形成的电场中,画一正方形ABCD,对角线AC与两点电荷连线重合,两对角线交点O恰为电荷连线的中点.下列说法中正确的是( )
 如图所示,在等量异种电荷形成的电场中,画一正方形ABCD,对角线AC与两点电荷连线重合,两对角线交点O恰为电荷连线的中点.下列说法中正确的是( )
如图所示,在等量异种电荷形成的电场中,画一正方形ABCD,对角线AC与两点电荷连线重合,两对角线交点O恰为电荷连线的中点.下列说法中正确的是( )| A. | A点的电场强度等于B点的电场强度 | |
| B. | B、D两点的电场强度及电势均相同 | |
| C. | 一电子由B点沿B→C→D路径移至D点,电势能先减小后增大 | |
| D. | 一电子由C点沿C→O→A路径移至A点,电场力对其先做负功后做正功 |
 如图所示,实线为t1=0时刻的图象,虚线为t2=0.1s时刻的波形,试求:
如图所示,实线为t1=0时刻的图象,虚线为t2=0.1s时刻的波形,试求: 一矩形线圈,在匀强磁场中绕垂直磁感线的对称轴转动,形成如图所示的交变电动势图象,试根据图象求出:
一矩形线圈,在匀强磁场中绕垂直磁感线的对称轴转动,形成如图所示的交变电动势图象,试根据图象求出: 如图所示,在内壁光滑的平底玻璃管内,装有一质量为10g的小球(可视为质点),将玻璃管开口端封闭后安装在转轴O上,转轴到管底的距离为25cm,让玻璃管在竖直面内匀速转动,求:
如图所示,在内壁光滑的平底玻璃管内,装有一质量为10g的小球(可视为质点),将玻璃管开口端封闭后安装在转轴O上,转轴到管底的距离为25cm,让玻璃管在竖直面内匀速转动,求: