题目内容
3.在半径R=5000km的某星球表面,宇航员做了如下实验,实验装置如图甲所示,竖直平面内的光滑轨道由轨道AB和圆弧轨道BC组成,将质量m=0.2kg的小球从轨道AB上高H处的某点静止滑下,用力传感器测出小球经过C点时对轨道的压力F,改变H的大小,可测出相应的F的大小,F随H的变化关系如图乙所示,求:
(1)圆轨道的半径.
(2)该星球的第一宇宙速度.
分析 (1)小球从A到C运动的过程中,只有重力做功,机械能守恒,根据机械能守恒定律和牛顿第二定律求出小球对轨道C点的压力与H的关系式,然后结合F-H图线求出圆轨道的半径.
(2)第一宇宙速度与贴着星球表面做匀速圆周运动的速度相等,根据万有引力等于重力,求出该星球的第一宇宙速度.
解答 解:
(1)设该星球表面的重力加速度为g0,圆轨道的半径为r.当H=0.4m时,小球恰能通过C点,此时F=0
由机械能守恒得:
mg0(H-2r)=$\frac{1}{2}$mv02
由圆周运动可得:mg0=m$\frac{{v}_{0}^{2}}{r}$
由以上各式解得:r=$\frac{2}{5}$H=2 m
(2)当H1=10m时,
mg0(H1-2r)=$\frac{1}{2}$mv2
mg0+F=m$\frac{{v}^{2}}{r}$
由F-H图象可得:g0=5m/s2
根据万有引力定律和向心力公式有:G$\frac{Mm}{{R}^{2}}$=m$\frac{{v}^{2}}{R}$
G$\frac{Mm}{{R}^{2}}$=mg0
由⑦⑧⑨得该星球的第一宇宙速度:v=$\sqrt{{g}_{0}R}$=$\sqrt{5×5000×1{0}^{3}}$=5×103m/s=5km/s.
答:(1)圆弧轨道BC的半径为2m.
(2)该星球的第一宇宙速度为5km/s
点评 本题是牛顿运动定律与机械能守恒定律的综合题,解决本题的关键根据该规律得出压力F与H的关系式.

练习册系列答案
相关题目
13. 以不同的抛射角抛出三个小球A、B、C,三球在空中的运动轨迹如图所示,下列说法中正确的是( )
以不同的抛射角抛出三个小球A、B、C,三球在空中的运动轨迹如图所示,下列说法中正确的是( )
 以不同的抛射角抛出三个小球A、B、C,三球在空中的运动轨迹如图所示,下列说法中正确的是( )
以不同的抛射角抛出三个小球A、B、C,三球在空中的运动轨迹如图所示,下列说法中正确的是( )| A. | A、B、C三球在运动过程中,加速度都相同 | |
| B. | B球的射程最远,所以最迟落地 | |
| C. | A球的射高最大,所以最迟落地 | |
| D. | A、C两球的水平位移相等,所以两球的水平速度分量相等 |
11. 两小球A和B,A球系在一根长为L的轻质细绳OA上,B球系在轻质橡皮绳OB上,现将两球都拉到如图所示的水平位置上,让两绳均拉直(此时橡皮绳为原长),然后无初速释放.不计空气阻力,当两球通过最低点时,橡皮绳与细绳等长.关于小球A和B,下列说法正确的是( )
两小球A和B,A球系在一根长为L的轻质细绳OA上,B球系在轻质橡皮绳OB上,现将两球都拉到如图所示的水平位置上,让两绳均拉直(此时橡皮绳为原长),然后无初速释放.不计空气阻力,当两球通过最低点时,橡皮绳与细绳等长.关于小球A和B,下列说法正确的是( )
 两小球A和B,A球系在一根长为L的轻质细绳OA上,B球系在轻质橡皮绳OB上,现将两球都拉到如图所示的水平位置上,让两绳均拉直(此时橡皮绳为原长),然后无初速释放.不计空气阻力,当两球通过最低点时,橡皮绳与细绳等长.关于小球A和B,下列说法正确的是( )
两小球A和B,A球系在一根长为L的轻质细绳OA上,B球系在轻质橡皮绳OB上,现将两球都拉到如图所示的水平位置上,让两绳均拉直(此时橡皮绳为原长),然后无初速释放.不计空气阻力,当两球通过最低点时,橡皮绳与细绳等长.关于小球A和B,下列说法正确的是( )| A. | 通过最低点时小球A的机械能大于小球B的机械能 | |
| B. | 两小球从释放至运动到最低点的全程中机械能均守恒 | |
| C. | 两小球从释放至运动到最低点的过程中重力的冲量一定相等 | |
| D. | 小球A运动到最低点时的速率大于小球B运动到该点的速率 |
18. 图中实线是一簇未标明方向的由点电荷产生的电场线,虚线是某一带电粒子通过该电场区域时的运动轨迹,a、b是轨迹上的两点.若带电粒子在运动中只受电场力作用,根据此图可作出正确判断的是( )
图中实线是一簇未标明方向的由点电荷产生的电场线,虚线是某一带电粒子通过该电场区域时的运动轨迹,a、b是轨迹上的两点.若带电粒子在运动中只受电场力作用,根据此图可作出正确判断的是( )
 图中实线是一簇未标明方向的由点电荷产生的电场线,虚线是某一带电粒子通过该电场区域时的运动轨迹,a、b是轨迹上的两点.若带电粒子在运动中只受电场力作用,根据此图可作出正确判断的是( )
图中实线是一簇未标明方向的由点电荷产生的电场线,虚线是某一带电粒子通过该电场区域时的运动轨迹,a、b是轨迹上的两点.若带电粒子在运动中只受电场力作用,根据此图可作出正确判断的是( )| A. | 带电粒子所带电荷一定为正 | |
| B. | 带电粒子的动能一定增大 | |
| C. | 带电粒子电势能一定增大 | |
| D. | 带电粒子在a点电势能一定小于b点的电势能 |
8. 一质量为2kg的质点在如图甲所示的xOy平面内运动,在x方向的速度时间图象和y方向的位移时间(y-t)图象分别如图乙、丙所示,由此可知( )
一质量为2kg的质点在如图甲所示的xOy平面内运动,在x方向的速度时间图象和y方向的位移时间(y-t)图象分别如图乙、丙所示,由此可知( )
 一质量为2kg的质点在如图甲所示的xOy平面内运动,在x方向的速度时间图象和y方向的位移时间(y-t)图象分别如图乙、丙所示,由此可知( )
一质量为2kg的质点在如图甲所示的xOy平面内运动,在x方向的速度时间图象和y方向的位移时间(y-t)图象分别如图乙、丙所示,由此可知( )| A. | t=0s时,质点的速度大小为12m/s | B. | 质点做加速度恒定的曲线运动 | ||
| C. | 前两秒,质点所受的合力大小为10N | D. | t=1.0s时,质点的速度大小为7m/s |
15.下列说法正确的是 ( )
| A. | 分子间的距离增大时,分子势能一定增大 | |
| B. | 晶体有确定的熔点,非晶体没有确定的熔点 | |
| C. | 热量总是白发地从分子平均动能大的物体传递到分子平均动能小的物体 | |
| D. | 物体吸热时,它的内能一定增加 | |
| E. | 一定质量的理想气体,如果压强不变,体积增大,那么它一定从外界吸热 |
12.下列核反应方程式中,X代表α粒子(${\;}_{2}^{4}He$)的反应式是( )
| A. | ${\;}_{2}^{4}He$+${\;}_{4}^{9}Be$→${\;}_{6}^{12}C$+X | B. | ${\;}_{90}^{234}Th$→${\;}_{91}^{234}Pa$+X | ||
| C. | ${\;}_{1}^{2}H$+${\;}_{1}^{3}H$→${\;}_{0}^{1}n$+X | D. | ${\;}_{15}^{30}P$→${\;}_{14}^{30}Si$+X |
 ”形状金属杆MNPQGH在辐向磁场中也以角速度ω匀速转动,如图乙所示,图丙为发电机的截面图,已知NP=GQ=R,PQ=L,MH两端接入电阻r,其余电阻不计.
”形状金属杆MNPQGH在辐向磁场中也以角速度ω匀速转动,如图乙所示,图丙为发电机的截面图,已知NP=GQ=R,PQ=L,MH两端接入电阻r,其余电阻不计.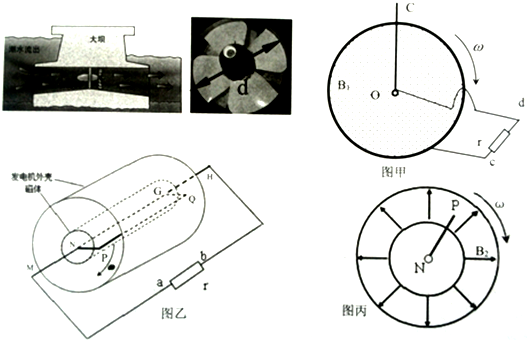
 木块B放在水平地面上,木块B的质量为0.2kg,在木板上放一质量为1.3kg的A物体A与木板B间、木板与地面间的摩擦因数均为0.4,用水平拉力F将木板B匀速拉出,绳与水平方向成37°.问绳的拉力T多大?水平拉力多大?(tan37°=0.6,cos37°=0.8,g=10m/s2)
木块B放在水平地面上,木块B的质量为0.2kg,在木板上放一质量为1.3kg的A物体A与木板B间、木板与地面间的摩擦因数均为0.4,用水平拉力F将木板B匀速拉出,绳与水平方向成37°.问绳的拉力T多大?水平拉力多大?(tan37°=0.6,cos37°=0.8,g=10m/s2)