题目内容
如图，质量为m1的物体A经一轻质弹簧与下方地面上的质量为m2的物体B相连，弹簧的劲度系数为k，A、B都处于静止状态，一条不可伸长的轻绳绕过轻滑轮，一端连物体A，另一端连一轻挂钩，开始时各段绳都处于伸直状态，A上方的一段绳沿竖直方向．现在挂钩上挂一质量为m3的物体C并从静止状态释放，已知它恰好能使B离开地面但不继续上升．若将C换成另一个质量为(m1＋m3)的物体D，仍从上述初始位置由静止状态释放，则这次B刚离地时D的速度的大小是多少？(已知重力加速度为g)
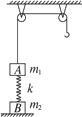
解析：
|
解析：解决问题的关键在于搞清系统中动能和势能的转化关系．本题描述的物理情景有三个过程：(1)挂C以前，A、B都静止在地面上，弹簧处于压缩状态，压缩量设为x1；(2)挂C后到B恰好离开地面的过程中，B不再继续，隐含A、C的末速度也刚好为零，此过程中，A上升，弹簧伸长达到伸长状态，设弹簧的伸长量为x2，则A升高(x1＋x2)，C同时降低(x1＋x2)，这一过程中，弹簧弹性势能的增加量ΔE来源于A、C重力势能的减少量；(3)换挂D后，B刚好离开地面时的速度仍为零，与此同一瞬间A、D的速度大小相等，弹簧弹性势能的增加量ΔE仍与过程(2)中的相同．A、C重力势能的减少量一部分用于增加系统动能，另一部分用于增加弹簧的弹性势能ΔE． 开始时，A、B静止，设弹簧压缩量为x1，有 kx1＝m1g ① 挂C并释放后，C向下运动，A向上运动，设B刚要离地时弹簧伸长量为x2，有 kx1＝m2g ② B不再上升，表示此时A和C的速度为零，C已降到其最低点，由机械能守恒，与初始状态相比，弹簧弹性势能的增加量为 ΔE＝m3g(x1＋x2)－m1g(x1＋x2) ③ C换成D后，当B刚离地时弹簧势能的增量与前一次相同，由能量关系得 由③④式得 由①②⑤式得v＝ 方法归纳：本题只有重力和系统内的弹力(弹簧弹力和绳的弹力)做功，系统机械能守恒．解决这一问题可以采用某一状态的机械能等于另一状态的机械能，但这种方法涉及要选取零势能参考平面．而采用势能的减少量等于动能的增加量这一方法较好，它不必选取零势能参考平面，但这种方法一定要搞清能量间的转化关系．另外还要注意挖掘题目的隐含条件． |
(m3＋m1)v2＋
．
轻巧夺冠周测月考直通高考系列答案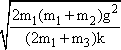
如图所示，倾角为θ的直角斜面体固定在水平地面上，其顶端固定有一轻质定滑轮，轻质弹簧和轻质细绳相连，一端接质量为m2的物块B，物块B放在地面上且使滑轮和物块间的细绳竖直，一端连接质量为m1的物块A，物块A放在光滑斜面上的P点保持静止，弹簧和斜面平行，此时弹簧具有的弹性势能为Ep．不计定滑轮、细绳、弹簧的质量，不计斜面、滑轮的摩擦，已知弹簧劲度系数为k，P点到斜面底端的距离为L．现将物块A缓慢斜向上移动，直到弹簧刚恢复原长时的位置，并由静止释放物块A，当物块B刚要离开地面时，物块A的速度即变为零，求：
如图所示，小圆环A系着一个质量为m2的物块并套在另一个竖直放置的大圆环上，有一细线一端拴在小圆环A上，另一端跨过固定在大圆环最高点B的一个小滑轮后吊着一个质量为m1的物块．如果小圆环、滑轮、绳子的大小和质量以及相互之间的摩擦都可以忽略不计，绳子又不可伸长，若平衡时弦AB所对应的圆心角为α，则两物块的质量比m1：m2应为（ ）
如图所示，已知轻弹簧发生弹性形变时所具有的弹性势能Ep=
如图所示，小圆环A系着一个质量为m2的物块并套在另一个竖直放置的大圆环上，有一细线一端拴在小圆环A上，另一端跨过固定在大圆环最高点B的一个小滑轮后吊着一个质量为m1的物块．如果小圆环、滑轮、绳子的大小和质量以及相互之间的摩擦都可以忽略不计，绳子又不可伸长，若平衡时弦AB所对应的圆心角为α，则两物块的质量比m1：m2应为（ ）