题目内容
18.如图所示,用密度为d、电阻率为ρ、横截面积为A的粗金属丝制成边长为 L的闭合正方形框abb′a′,金属方框水平放在磁极的狭缝间,方框平面与磁场方向平行,如图1、图2所示.设匀强磁场仅存在于相对磁极之间,其它地方的磁场忽略不计.可认为方框的aa′边和 bb′边都处在磁极间,极间磁感应强度大小为B.方框从静止开始释放,其平面在下落过程中保持水平(不计空气阻力).假设磁场区域在竖直方向足够长,试求:
(1)方框下落的速度为v时的电功率
(2)方框下落的最终速度
(3)当下落高度h时,方框速度达到最大,从开始下落到速度达到最大过程方框消耗的电能.
分析 (1)根据切割产生的感应电动势,抓住切割的有效长度求出感应电动势的大小,通过闭合电路欧姆定律求出电流的大小,从而求出方框下落的速度为v时的电功率.
(2)当重力等于安培力时,速度最大,根据平衡,结合切割产生的感应电动势公式、闭合电路欧姆定律以及安培力大小公式求出最终的速度大小.
(3)根据能量守恒定律,即可求解.
解答 解:(1)由题意知,方框所在处在磁感应强度为B;当环速度为v时,切割磁感线产生的电动势为:
E=2BLv;
电流为:I=$\frac{E}{\frac{ρ•4L}{A}}$=$\frac{EA}{4ρL}$
电功率为:P=I2R电=($\frac{EA}{4ρL}$)2×$\frac{ρ•4L}{A}$=$\frac{{E}^{2}A}{4ρL}$=$\frac{{B}^{2}LA{v}^{2}}{ρ}$
(2)当方框加速度为零时,有最大速度vm
此时有:F安=2BIL=B×$\frac{2BL{v}_{m}}{ρ\frac{4L}{A}}×L$=$\frac{{B}^{2}LA{v}_{m}}{2ρ}$
由平衡条件有:mg=F安
又m=dLA
联立上式,解得:vm=$\frac{2ρdg}{{B}^{2}}$
(3)由能量守恒定律:
mgh=$\frac{1}{2}$mvm2+Q
解得:Q=mgh-$\frac{1}{2}$mvm2=dLA(gh-$\frac{2{ρ}^{2}{d}^{2}{g}^{2}}{{B}^{4}}$);
答:(1)方框下落的速度为v时的电功率$\frac{{B}^{2}LA{v}^{2}}{ρ}$;
(2)方框下落的最终速度$\frac{2ρdg}{{B}^{2}}$;
(3)从开始下落到速度达到最大过程方框消耗的电能dLA(gh-$\frac{2{ρ}^{2}{d}^{2}{g}^{2}}{{B}^{4}}$).
点评 本题考查电磁感应与力学以及能量的综合,掌握切割产生的感应电动势公式、闭合电路欧姆定律等知识,知道当重力等于安培力时,速度最大.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 液体温度越高,布朗运动越剧烈 | |
| B. | 悬浮粒子越大,布朗运动越剧烈 | |
| C. | 布朗运动是由于液体各部分的温度不同而引起的 | |
| D. | 布朗运动就是液体分子的无规则运动 |
 如图所示,垂直纸面的正方形匀强磁场区域内,有一位于纸面且电阻均匀的正方形导体框abcd,现将导体框分别朝两个方向以v、3v速度匀速拉出磁场,则导体框从两个方向移出磁场的两过程中,下列说法中正确的是( )
如图所示,垂直纸面的正方形匀强磁场区域内,有一位于纸面且电阻均匀的正方形导体框abcd,现将导体框分别朝两个方向以v、3v速度匀速拉出磁场,则导体框从两个方向移出磁场的两过程中,下列说法中正确的是( )| A. | 导体框所受安培力方向相同 | B. | 导体框中产生的感应电流方向相同 | ||
| C. | 导体框ad边两端电势差相等 | D. | 通过导体框截面的电荷量不相同 |
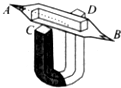 如图所示是用阴极射线管演示电子在磁场中受洛伦兹力的实验装置,图中虚线是电子的运动轨迹,那么下列关于此装置的说法正确的是( )
如图所示是用阴极射线管演示电子在磁场中受洛伦兹力的实验装置,图中虚线是电子的运动轨迹,那么下列关于此装置的说法正确的是( )| A. | A端接的是高压直流电源的正极 | B. | C端是蹄形磁铁的N极 | ||
| C. | C端是蹄形磁铁的S极 | D. | 以上说法均不对 |
 如图所示,长度为0.5m的轻质细杆OA,A端固定一质量为3kg的小球,以O点为圆心,在竖直平面内做圆周运动,若小球通过最高点时的速度为2m/s,取g=10m/s2,则此时轻杆OA受到小球的作用力为( )
如图所示,长度为0.5m的轻质细杆OA,A端固定一质量为3kg的小球,以O点为圆心,在竖直平面内做圆周运动,若小球通过最高点时的速度为2m/s,取g=10m/s2,则此时轻杆OA受到小球的作用力为( )| A. | 6N的拉力 | B. | 6N的压力 | C. | 54N的拉力 | D. | 54N的压力 |
 如图所示,在水平面上固定着三个完全相同的木块,一子弹以水平速度v0射入木块,若子弹在木块中做匀减速直线运动,当穿透第三个木块时速度恰好为零,则子弹依次射入每个木块时的速度v1、v2、v3之比和穿过每个木块所用的时间t1、t2、t3之比分别为( )
如图所示,在水平面上固定着三个完全相同的木块,一子弹以水平速度v0射入木块,若子弹在木块中做匀减速直线运动,当穿透第三个木块时速度恰好为零,则子弹依次射入每个木块时的速度v1、v2、v3之比和穿过每个木块所用的时间t1、t2、t3之比分别为( )| A. | v1:v2:v3=1:2:3 | B. | v1:v2:v3=$\sqrt{3}:\sqrt{2}$:1 | ||
| C. | t1:t2:t3=1:$\sqrt{2}:\sqrt{3}$ | D. | t1:t2:t3=($\sqrt{3}$-$\sqrt{2}$):($\sqrt{2}$-1):1 |
 质量为m的通电细杆ab置于倾角为θ的平行导轨上,导轨宽为d,杆与导轨间的摩擦因数为μ,有电流时ab恰好在导轨上静止,如图所示.下图是从右侧观察时的四种不同的匀强磁场方向下的四个平面图,其中通电细杆ab与导轨间的摩擦力不可能为零的是( )
质量为m的通电细杆ab置于倾角为θ的平行导轨上,导轨宽为d,杆与导轨间的摩擦因数为μ,有电流时ab恰好在导轨上静止,如图所示.下图是从右侧观察时的四种不同的匀强磁场方向下的四个平面图,其中通电细杆ab与导轨间的摩擦力不可能为零的是( )



 滑雪是一项惊险又刺激的运动.某滑雪场的滑道如图所示,AB为倾角θ=37°的斜滑道,BC为高h=0.8m的竖直山坡,CD为水平滑道.有一滑雪者从A点由静止滑下.到B点经一小段不计长度的圆弧后水平滑出,落在了水平滑道的D点,已知滑雪板与滑道间的动摩擦因数μ=0.15,落点D与C之间的距离为9.6m.不计空气阻力,g=10m/s2,sin37°=0.6,cos37°=0.8.求:
滑雪是一项惊险又刺激的运动.某滑雪场的滑道如图所示,AB为倾角θ=37°的斜滑道,BC为高h=0.8m的竖直山坡,CD为水平滑道.有一滑雪者从A点由静止滑下.到B点经一小段不计长度的圆弧后水平滑出,落在了水平滑道的D点,已知滑雪板与滑道间的动摩擦因数μ=0.15,落点D与C之间的距离为9.6m.不计空气阻力,g=10m/s2,sin37°=0.6,cos37°=0.8.求: 如图所示,质量均为m的小车与木箱紧挨着静止在光滑的水平冰面上,质量为2m的小明站在小车上用力向右迅速推出木箱后,木箱相对于冰面的速度为v,接着木箱与右侧竖直墙壁发生弹性碰撞,反弹后被小明接住,求
如图所示,质量均为m的小车与木箱紧挨着静止在光滑的水平冰面上,质量为2m的小明站在小车上用力向右迅速推出木箱后,木箱相对于冰面的速度为v,接着木箱与右侧竖直墙壁发生弹性碰撞,反弹后被小明接住,求