题目内容
 (2006?盐城一模)如图所示,竖直的光滑杆上套着一轻质弹簧,弹簧长度为原长时,上端在O点处.现将质量,m2=3kg的圆环套在杆上,压缩弹簧,平衡于A点处,A点和O点间距为x0;再将一质量m1=6kg的圆环套在杆上,从距A点3x0处的B点由静止开始下滑并与m2碰撞后粘为一体.它们运动到C处时速度达到最大值,此时动能Ek=19.5J.已知弹簧劲度系数k=300N/m.求:
(2006?盐城一模)如图所示,竖直的光滑杆上套着一轻质弹簧,弹簧长度为原长时,上端在O点处.现将质量,m2=3kg的圆环套在杆上,压缩弹簧,平衡于A点处,A点和O点间距为x0;再将一质量m1=6kg的圆环套在杆上,从距A点3x0处的B点由静止开始下滑并与m2碰撞后粘为一体.它们运动到C处时速度达到最大值,此时动能Ek=19.5J.已知弹簧劲度系数k=300N/m.求:(1)m1在与m2碰撞前瞬间的速度v;
(2)m1与m2经过C点时,弹簧的弹性势能Ep.
分析:(1)对m2进行受力分析,由平衡条件及胡克定律求出x0,对m1应用动能定理可以求出两圆环碰撞前m1的速度.
(2)两圆环碰撞过程中动量守恒,由动量守恒定律可以求出碰后两圆环的速度,求出碰撞过程中损失的机械能;
当两圆环所受合力为零时,两圆环的速度最大,动能最大,由能量守恒定律可以求出此时弹簧的弹性势能.
(2)两圆环碰撞过程中动量守恒,由动量守恒定律可以求出碰后两圆环的速度,求出碰撞过程中损失的机械能;
当两圆环所受合力为零时,两圆环的速度最大,动能最大,由能量守恒定律可以求出此时弹簧的弹性势能.
解答:解:(1)对m2由碰后条件得:m2g=kx0,解得:x0=0.1m;
m1从B落到A点过程中,由动能定理得:
m1g×3x0=
m1v02-0,解得:v0=
m/s;
(2)两圆环碰撞过程中动量守恒,由动量守恒定律可得:
m1v0=(m1+m2)v1,
碰撞过程中系统损失的机械能:
△E=
m1v02-
(m1+m2)v12,
解得:△E=6J;
两圆环到达C点时,kx=(m1+m2)g,
x1=x-x0,解得:x1=0.2m,
由能量守恒定律可得:
m1g(3x0+x1)+m2g(x0+x1)-△E=EK+EP,
解得:EP=13.5J;
答:(1)m1在与m2碰撞前瞬间的速度为
m/s;
(2)m1与m2经过C点时,弹簧的弹性势能为你13.5J.
m1从B落到A点过程中,由动能定理得:
m1g×3x0=
| 1 |
| 2 |
| 6 |
(2)两圆环碰撞过程中动量守恒,由动量守恒定律可得:
m1v0=(m1+m2)v1,
碰撞过程中系统损失的机械能:
△E=
| 1 |
| 2 |
| 1 |
| 2 |
解得:△E=6J;
两圆环到达C点时,kx=(m1+m2)g,
x1=x-x0,解得:x1=0.2m,
由能量守恒定律可得:
m1g(3x0+x1)+m2g(x0+x1)-△E=EK+EP,
解得:EP=13.5J;
答:(1)m1在与m2碰撞前瞬间的速度为
| 6 |
(2)m1与m2经过C点时,弹簧的弹性势能为你13.5J.
点评:本题考查了求圆环的速度、弹簧的弹性势能等问题,分析清楚运动过程、应用动能定理、动量守恒定律、平衡条件、能量守恒定律即可正确解题.

练习册系列答案
相关题目
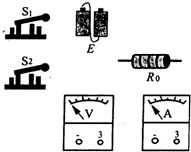 (2006?盐城一模)某同学准备测定一只量程已知的电压表的内阻,提供的器材及规格如下:
(2006?盐城一模)某同学准备测定一只量程已知的电压表的内阻,提供的器材及规格如下: (2006?盐城一模)如图所示,间距为d的两平行板之间有方向向右的匀强电场,正方形容器abcd内有方向垂直纸面向里的匀强磁场,O为ab边的中点,ab边紧靠平行板.有两个质量均为m,电量均为q的带电粒子P1和P2在小孔处以初速度为零先后释放.P1经匀强电场加速后,从O处垂直正方形的ab边进入匀强磁场中,每一次和边碰撞时速度方向都垂直于被碰的边,当P1刚好回到O处时与后释放的P2相碰,以后P1、P2都在O处相碰.假设所有碰撞过程均无机械能损失.
(2006?盐城一模)如图所示,间距为d的两平行板之间有方向向右的匀强电场,正方形容器abcd内有方向垂直纸面向里的匀强磁场,O为ab边的中点,ab边紧靠平行板.有两个质量均为m,电量均为q的带电粒子P1和P2在小孔处以初速度为零先后释放.P1经匀强电场加速后,从O处垂直正方形的ab边进入匀强磁场中,每一次和边碰撞时速度方向都垂直于被碰的边,当P1刚好回到O处时与后释放的P2相碰,以后P1、P2都在O处相碰.假设所有碰撞过程均无机械能损失.