题目内容
如图所示,在水平圆盘上有一过圆心的光滑小槽,槽内有两根原长、劲度系数均相同的橡皮绳拉住一质量为m的小球,其中O点为圆盘的中心, 点为圆盘的边缘.橡皮绳的劲度系数为k,原长为圆盘半径及的
点为圆盘的边缘.橡皮绳的劲度系数为k,原长为圆盘半径及的 .现使圆盘角速度由零缓慢增大,求圆盘的角速度
.现使圆盘角速度由零缓慢增大,求圆盘的角速度 与
与 时,小球所对应的线速度之比.
时,小球所对应的线速度之比.

答案:略
解析:
解析:
|
当橡皮绳 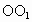 拉伸而 拉伸而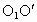 刚好被拉直时.设小球做匀速圆周运动角速度为 刚好被拉直时.设小球做匀速圆周运动角速度为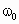 . .
由牛顿第二定律有: 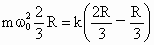 , ,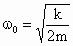 . .
当 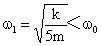 时,橡皮绳 时,橡皮绳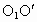 拉伸, 拉伸,
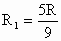 . .
当 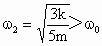 时,此时橡皮绳 时,此时橡皮绳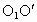 松弛. 松弛.
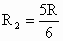 . .
所以 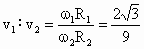 . .
求解本题时,首先要判断圆盘以不同角速度转动时,橡皮绳是处在拉伸还是松弛状态.为判断橡皮绳是拉伸还是松弛,应求出橡皮绳 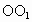 拉伸而橡皮绳 拉伸而橡皮绳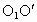 刚好被拉直时对应的临界角速度 刚好被拉直时对应的临界角速度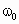 .将实际角速度与临界角速度 .将实际角速度与临界角速度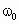 进行比较.用牛顿第二定律列出圆盘以不同角速度转动时小球所满足的动力学方程. 进行比较.用牛顿第二定律列出圆盘以不同角速度转动时小球所满足的动力学方程.
物体做变速圆周运动时,必须充分注意到可能发生离心运动和向心运动两种情况,如果是形变明显的橡皮条、弹簧提供向心力时,一定会随着角速度的减小或增大而发生向心运动和离心运动,直至以新的角速度在新的半径上做匀速圆周运动.当然也存在着不会再做圆周运动的可能. 因小球做匀速圆周运动,橡皮绳 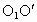 必须始终处在拉伸状态.橡皮绳 必须始终处在拉伸状态.橡皮绳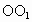 ,刚好拉直而未拉紧时是小球做圆周运动的一个临界状态.求出此状态下对应的角速度 ,刚好拉直而未拉紧时是小球做圆周运动的一个临界状态.求出此状态下对应的角速度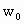 .实际角速度比临界角速度 .实际角速度比临界角速度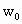 大时,橡皮绳 大时,橡皮绳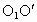 松弛,实际角速度比临界角速度 松弛,实际角速度比临界角速度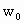 小时,两橡皮绳均处于拉伸状态. 小时,两橡皮绳均处于拉伸状态. |

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
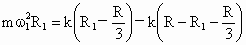
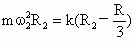
 如图所示,在水平圆盘上沿半径方向放置用细线相连的质量均为m的A、B两个物块(可视为质点),A和B距轴心O的距离分别为rA=R,rB=2R,且A、B与转盘之间的最大静摩擦力都是fm,两物块随着圆盘转动始终与圆盘保持相对静止.则圆盘转动的角速度从0逐渐增大的过程中,下列说法正确的是( )
如图所示,在水平圆盘上沿半径方向放置用细线相连的质量均为m的A、B两个物块(可视为质点),A和B距轴心O的距离分别为rA=R,rB=2R,且A、B与转盘之间的最大静摩擦力都是fm,两物块随着圆盘转动始终与圆盘保持相对静止.则圆盘转动的角速度从0逐渐增大的过程中,下列说法正确的是( ) 如图所示,在水平圆盘上有一过圆心的光滑圆槽,槽内有两根相同的橡皮绳拉住一质量为m的小球(可以视为质点),其中O点为圆盘中心,O′点为圆盘边缘.橡皮绳的劲度系数为k(类似弹簧遵从胡克定律),原长为圆半径R的1/3,现使圆盘的角速度由零开始缓慢增大,求圆盘的角速度为ω1=
如图所示,在水平圆盘上有一过圆心的光滑圆槽,槽内有两根相同的橡皮绳拉住一质量为m的小球(可以视为质点),其中O点为圆盘中心,O′点为圆盘边缘.橡皮绳的劲度系数为k(类似弹簧遵从胡克定律),原长为圆半径R的1/3,现使圆盘的角速度由零开始缓慢增大,求圆盘的角速度为ω1= 如图所示,在水平圆盘上沿半径方向放置用细线相连的质量均为m的A、B两个物块(可视为质点). A和B距轴心O的距离分别为rA=R,rB=2R,且A、B与转盘之间的最大静摩擦力都是fm,两物块A和B随着圆盘转动时,始终与圆盘保持相对静止.则在圆盘转动的角速度从0缓慢增大的过程中,下列说法正确的是( )
如图所示,在水平圆盘上沿半径方向放置用细线相连的质量均为m的A、B两个物块(可视为质点). A和B距轴心O的距离分别为rA=R,rB=2R,且A、B与转盘之间的最大静摩擦力都是fm,两物块A和B随着圆盘转动时,始终与圆盘保持相对静止.则在圆盘转动的角速度从0缓慢增大的过程中,下列说法正确的是( ) 如图所示,在水平圆盘上有一过圆心的光滑圆槽,槽内有两根相同的橡皮绳拉住一质量为m的小球(可以视为质点),其中O点为圆盘中心,O′点为圆盘边缘.橡皮绳的劲度系数为k(类似弹簧遵从胡克定律),原长为圆半径R的1/3,现使圆盘的角速度由零开始缓慢增大,求圆盘的角速度为ω1=
如图所示,在水平圆盘上有一过圆心的光滑圆槽,槽内有两根相同的橡皮绳拉住一质量为m的小球(可以视为质点),其中O点为圆盘中心,O′点为圆盘边缘.橡皮绳的劲度系数为k(类似弹簧遵从胡克定律),原长为圆半径R的1/3,现使圆盘的角速度由零开始缓慢增大,求圆盘的角速度为ω1= 与ω2=
与ω2= 时,小球所对应的线速度之比v1:v2.
时,小球所对应的线速度之比v1:v2. 与ω2=
与ω2= 时,小球所对应的线速度之比v1:v2.
时,小球所对应的线速度之比v1:v2.