题目内容
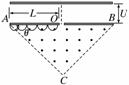
如图所示，在一底边长为2L，θ＝45°的等腰三角形区域内(O为底边中点)有垂直纸面向外的匀强磁场。现有一质量为m、电量为q的带正电粒子从静止开始经过电势差为U的电场加速后，从O点垂直于AB进入磁场，不计重力与空气阻力的影响。求
（1）粒子经电场加速射入磁场时的速度大小；
（2）磁感应强度B为多少时，粒子能以最大的圆周半径偏转后打到OA板；
（3）增大磁感应强度B，可延长粒子在磁场中的运动时间，求粒子在磁场中运动的最长时间。(不计粒子与AB板碰撞的作用时间，设粒子与AB板碰撞前后，电量保持不变并以相同的速率反弹)
解： (1)粒子经电场加速射入磁场时的速度为v
由qU＝
mv2 得v＝ 
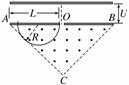
(2)要使圆周半径最大，则粒子的圆周轨迹应与AC边相切，设圆周半径为R
由图中几何关系：
R＋
＝L
由qvB＝m
得B＝
(3)设粒子运动圆周半径为r，r＝
，当r越小，最后一次打到AB板的点越靠近A端点，在磁场中圆周运动累积路程越大，时间越长。当r为无穷小，经过n个半圆运动，最后一次打到A点。有：n＝
圆周运动周期：T＝
最长的时间：tm＝n
得：tm＝
＝
答案：(1) (2) (3)
练习册系列答案
相关题目
（2011?山西模拟）如图所示，在一底边长为2a，θ=30°的等腰三角形区域内（D在底边中点），有垂直纸面向外的匀强磁场．现有一质量为m，电量为q的带正电粒子从静止开始经过电势差为U的电场加速后，从D点垂直于EF进入磁场，不计重力和与空气阻力的影响．
（2013?山西模拟）如图所示，在一底边长为2L、髙为L的等腰直角三角形区域分布着如图所示的匀强 磁场，左侧磁场方向垂直纸面向外．右侧磁场方向垂直纸面向里，磁感应强度大小均为 B．一边长为L、总电阻为R的正方形导线框必abcd，从图示位置开始沿x轴E方向以速 率v匀速运动并穿过磁场区域．取沿a→b→c→d→a方向．的感应电流 为正，则图乙中表示线框中电流i随 bc边的位置坐标x变化的图象正确 的是（ ）
如图所示，在一底边长为2L，θ=45°的等腰三角形区域内（O为底边中点）有垂直纸面向外的匀强磁场．现有一质量为m，电量为q的带正电粒子从静止开始经过电势差为U的电场加速后，从O点垂直于AB进入磁场，不计重力与空气阻力的影响．
如图所示，在一底边长为2L，θ=45°的等腰三角形区域内（O为B边中点）有垂直纸面向外的匀强磁场．现有一质量为m，电量为q的带负电粒子从静止由A板开始经过电势差为U的电场加速后，从O点垂直于B进入磁场，不计重力与空气阻力的影响．
，
°的等腰三角形区域内（D在底边中点，）有垂直纸面向外的匀强磁场，现有一质量为m，电量为q的带正电粒子从静止开始经过电势差为U的电场加速后，从D点垂直于EF进入磁场，不计重力和空气阻力的影响。