题目内容
16. 半径为2R的$\frac{1}{4}$圆轨道和半径为R的半圆轨道在最低点B平滑连接在一起,轨道固定在竖直平面内,处于同一水平面上的A、C两点分别是两个轨道的最高点,如图所示.一质量为m的小滑块P从A点由静止释放,到达最低点时与静止在该处的另一完全相同的小滑块Q发生碰撞,碰撞引爆了原来涂在两个滑块接触面上的少量火药,P、Q在很短时间内分开,经一段时间Q运动至C点,此时对轨道的压力大小等于4mg(g为重力加速度).不计轨道的摩擦.求:
半径为2R的$\frac{1}{4}$圆轨道和半径为R的半圆轨道在最低点B平滑连接在一起,轨道固定在竖直平面内,处于同一水平面上的A、C两点分别是两个轨道的最高点,如图所示.一质量为m的小滑块P从A点由静止释放,到达最低点时与静止在该处的另一完全相同的小滑块Q发生碰撞,碰撞引爆了原来涂在两个滑块接触面上的少量火药,P、Q在很短时间内分开,经一段时间Q运动至C点,此时对轨道的压力大小等于4mg(g为重力加速度).不计轨道的摩擦.求:(1)碰撞前滑块P的速度.
(2)P、Q分开瞬间Q的速度.
(3)P、Q相互作用过程,P、Q组成的系统机械能的增量.
分析 (1)碰撞前滑块P下滑过程中只有重力做功,机械能守恒,根据守恒定律列式求解;
(2)Q运动到C的过程中,机械能守恒定律,根据守恒定律列式;在C点,弹力和重力的合力提供向心力,根据牛顿第二定律列式;最后联立求解即可;
(3)P、Q相互作用过程,系统动量守恒,根据动量守恒定律列式;然后根据机械能的定义列式求解.
解答 解:(1)滑块P下滑过程,由机械能守恒定律,有:
mg•2R=$\frac{1}{2}m{v}^{2}$
解得:$v=2\sqrt{gR}$
(2)P、Q分开后,Q从B点滑至C点过程,根据机械能守恒定律,有:
$\frac{1}{2}m{v}_{Q}^{2}=mg•2R+\frac{1}{2}m{v}_{C}^{2}$
经过C点时,有:${F}_{C}+mg=m\frac{{v}_{C}^{2}}{R}$
将Fc=4mg代入可得P、Q分开瞬间Q的速度:
${v}_{Q}=3\sqrt{gR}$
(3)P、Q相互作用过程,由动量守恒定律,有:
mv=mvQ+mvP
P、Q系统机械能的增加量为:
$△E=\frac{1}{2}m{v}_{Q}^{2}+\frac{1}{2}m{v}_{P}^{2}-\frac{1}{2}m{v}^{2}$
联立解得:
△E=3mgR
答:(1)碰撞前滑块P的速度为2$\sqrt{gR}$.
(2)P、Q分开瞬间Q的速度为3$\sqrt{gR}$.
(3)P、Q相互作用过程,P、Q组成的系统机械能的增量为3mgR.
点评 本题关键是明确两个滑块的受力情况、运动情况,然后结合动量守恒定律、机械能守恒定律列式求解,不难.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
4.甲的重力是乙的3倍,它们从同一地点同一高度处同时自由落体,则下列说法正确的是( )
| A. | 甲比乙先着地 | B. | 甲与乙的加速度一样大 | ||
| C. | 甲、乙同时着地 | D. | 无法确定谁先着地 |
11. 如图所示,与锌板相连的验电器的铝箔原来是闭合的,用弧光灯发出的紫外线照射到锌板,结果发现验电器的铝箔张开一个角度,对于以上实验,下列说法正确的是( )
如图所示,与锌板相连的验电器的铝箔原来是闭合的,用弧光灯发出的紫外线照射到锌板,结果发现验电器的铝箔张开一个角度,对于以上实验,下列说法正确的是( )
 如图所示,与锌板相连的验电器的铝箔原来是闭合的,用弧光灯发出的紫外线照射到锌板,结果发现验电器的铝箔张开一个角度,对于以上实验,下列说法正确的是( )
如图所示,与锌板相连的验电器的铝箔原来是闭合的,用弧光灯发出的紫外线照射到锌板,结果发现验电器的铝箔张开一个角度,对于以上实验,下列说法正确的是( )| A. | 实验说明紫外线带电 | |
| B. | 实验说明紫外线能使锌板产生光电效应 | |
| C. | 验电器的铝箔带负电 | |
| D. | 验电器的铝箔带正电 |
8.某物体沿一直线运动,其v-t图象如图所示,则下列说法中正确的是( )
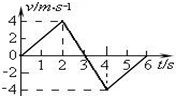

| A. | 第2s内和第3s内速度方向相反 | B. | 第2s内和第3s内的加速度方向相反 | ||
| C. | 第3s内速度方向与加速度方向相同 | D. | 第5s内速度方向与加速度方向相反 |
5.物体从静止开始做匀加速直线运动,第3秒内通过的位移是3m,则( )
| A. | 第3秒内的平均速度是3m/s | B. | 物体的加速度为1.2m/s2 | ||
| C. | 前3s内的位移是6m | D. | 3s 末的速度是3m/s |
 两平行金属板与电源相接,其间电场为匀强电场,K闭合后一带电微粒,自M板边缘垂直于电场方向射入.如图所示,在电场力作用下,发生偏转(重力忽略不计),恰好打在N板中央.M、N之间相距为d,为使微粒恰能飞出电场,N板至少应下移多少?(K一直闭合)
两平行金属板与电源相接,其间电场为匀强电场,K闭合后一带电微粒,自M板边缘垂直于电场方向射入.如图所示,在电场力作用下,发生偏转(重力忽略不计),恰好打在N板中央.M、N之间相距为d,为使微粒恰能飞出电场,N板至少应下移多少?(K一直闭合)