题目内容
质量为m的小物块A,放在质量为M的木板B的左端,B在水平拉力的作用下沿水平地面匀速向右滑动,且A、B相对静止.某时刻撤去水平拉力,经过一段时间,B在地面上滑行了一段距离x,A在B上相对于B向右滑行了一段距离L(设木板B足够长)后A和B都停下.已知A、B间的动摩擦因数μ1,B与地面间的动摩擦因数μ2,μ1>μ2,求x的表达式.

设A、B相对静止一起向右匀速运动时的速度为v.撤去外力后至停止的过程中,A受到的滑动摩擦力f1=μ1mg,加速度大a1=
=μ1g
此时B的加速度大小a2=
由于μ2>μ1,所 a2>μ2g>μ1g=a1
即木板B先停止后,A在木板上继续做匀减速运动,且其加速度大小不变.
对A应用动能定理-f1(L+x)=0-
mv2
对B应用动能定理 μ1mgx-μ2(m+M)gx=0-
Mv2
消去v解得x=
.
答:x的表达式是x=
.
| f1 |
| m1 |
此时B的加速度大小a2=
| μ2(m+M)g-μ1mg |
| M |
由于μ2>μ1,所 a2>μ2g>μ1g=a1
即木板B先停止后,A在木板上继续做匀减速运动,且其加速度大小不变.
对A应用动能定理-f1(L+x)=0-
| 1 |
| 2 |
对B应用动能定理 μ1mgx-μ2(m+M)gx=0-
| 1 |
| 2 |
消去v解得x=
| μML1 |
| (μ2-μ1)(m+M) |
答:x的表达式是x=
| μML1 |
| (μ2-μ1)(m+M) |

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 如图所示,EF为水平地面,O点左侧是粗糙的、右侧是光滑的.一轻质弹簧右端与墙壁固定,左侧与静止在O点质量为m的小物块A连接,弹簧处于原长状态.质量为4m的物块B在大小为F的水平恒力作用下由C处从静止开始向右运动,已知物块B与地面EO段间的滑动摩擦力大小为
如图所示,EF为水平地面,O点左侧是粗糙的、右侧是光滑的.一轻质弹簧右端与墙壁固定,左侧与静止在O点质量为m的小物块A连接,弹簧处于原长状态.质量为4m的物块B在大小为F的水平恒力作用下由C处从静止开始向右运动,已知物块B与地面EO段间的滑动摩擦力大小为
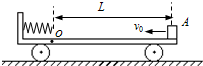 如图所示,质量为M的小车B静止在光滑水平面上,车的左端固定着一根弹簧,小车上O点以左部分光滑,O点以右部分粗糙,O点到小车右端长度为L.一质量为m的小物块A(可视为质点),以速度v0从小车右端向左滑动,与弹簧相碰,最后刚好未从小车右端滑出.求:
如图所示,质量为M的小车B静止在光滑水平面上,车的左端固定着一根弹簧,小车上O点以左部分光滑,O点以右部分粗糙,O点到小车右端长度为L.一质量为m的小物块A(可视为质点),以速度v0从小车右端向左滑动,与弹簧相碰,最后刚好未从小车右端滑出.求: 如图所示,在倾角为θ的固定的足够长斜面上静置一质量为m的小物块A,A与斜面之间的动摩擦因数为μ=tanθ.另有一底面光滑、质量为
如图所示,在倾角为θ的固定的足够长斜面上静置一质量为m的小物块A,A与斜面之间的动摩擦因数为μ=tanθ.另有一底面光滑、质量为