题目内容
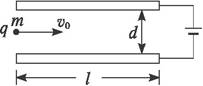
 质量为m、带电荷量为+q的小球以水平初速度v0进入竖直向上的匀强电场中,如图甲所示.今测得小球进入电场后在竖直方向上上升的高度y与水平方向的位移x之间的关系如图乙所示(重力加速度为g).根据图乙给出的信息,求小球在h高度处的动能.
质量为m、带电荷量为+q的小球以水平初速度v0进入竖直向上的匀强电场中,如图甲所示.今测得小球进入电场后在竖直方向上上升的高度y与水平方向的位移x之间的关系如图乙所示(重力加速度为g).根据图乙给出的信息,求小球在h高度处的动能.分析:小球受重力和电场力,在磁场中做类平抛运动,在垂直于磁场方向上做匀速直线运动,在沿电场方向上做匀加速直线运动,根据水平位移求出运动的时间,根据竖直位移求出加速度,再根据牛顿第二定律求出匀强电场的电场强度.
电场力是恒力,根据W=Fscosθ求出恒力的功.
根据动能定理求出小球在h高度处的动能.
电场力是恒力,根据W=Fscosθ求出恒力的功.
根据动能定理求出小球在h高度处的动能.
解答:解:小球进入电场后,水平方向做匀速直线运动,经时间t,则有:
水平方向:l=v0t
竖直方向:h=
解得:E=
+
由动能定理得:qEh-mgh=
-
m
得:Ek=
m
+
答:小球在h高度处的动能为
m
+
.
水平方向:l=v0t
竖直方向:h=
| (qE-mg)t2 |
| 2m |
解得:E=
| mg |
| q |
2hm
| ||
| ql2 |
由动能定理得:qEh-mgh=
| E | k |
| 1 |
| 2 |
| v | 2 0 |
得:Ek=
| 1 |
| 2 |
| v | 2 0 |
2m
| ||
| l2 |
答:小球在h高度处的动能为
| 1 |
| 2 |
| v | 2 0 |
2m
| ||
| l2 |
点评:带电粒子在电场中的运动可分为加速和偏转,加速类的题目由动能定理求解,而偏转类的题目一般考查运动的合成与分解的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,质量为m、带电荷量为+q的粒子,从两平行电极板正中央垂直电场线和磁感线以速度v飞入.已知两极间距为d,磁感应强度为B,这时粒子恰能沿直线穿过电场和磁场区域.今将磁感应强度增大到某值,则粒子将落到极板上.已知粒子重力不计,则粒子落到极板上时的动能为多少?
如图所示,质量为m、带电荷量为+q的粒子,从两平行电极板正中央垂直电场线和磁感线以速度v飞入.已知两极间距为d,磁感应强度为B,这时粒子恰能沿直线穿过电场和磁场区域.今将磁感应强度增大到某值,则粒子将落到极板上.已知粒子重力不计,则粒子落到极板上时的动能为多少? 如图所示,有一质量为m,带电荷量为+q的小球(可视为质点),自竖直向下、场强为E的匀强电场中的P点静止下落.在P点正下方距离h处有一弹性绝缘挡板S(挡板不影响匀强电场的分布),小球每次与挡板S相碰后电荷量均减少到碰前的k倍(k<1),而碰撞过程中小球的机械能不损失.
如图所示,有一质量为m,带电荷量为+q的小球(可视为质点),自竖直向下、场强为E的匀强电场中的P点静止下落.在P点正下方距离h处有一弹性绝缘挡板S(挡板不影响匀强电场的分布),小球每次与挡板S相碰后电荷量均减少到碰前的k倍(k<1),而碰撞过程中小球的机械能不损失.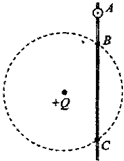 如图所示:光滑绝缘杆竖直放置,它与以正电荷Q为圆心的某一圆周交于B、C两点,质量为m,带电荷量为+q的有孔小球从杆上A点无初速下滑,已知q<Q,AB=h,小球滑到B点的速度大小为
如图所示:光滑绝缘杆竖直放置,它与以正电荷Q为圆心的某一圆周交于B、C两点,质量为m,带电荷量为+q的有孔小球从杆上A点无初速下滑,已知q<Q,AB=h,小球滑到B点的速度大小为