题目内容
15.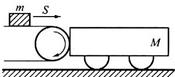 如图所示,水平传送带以v=12m/s的速度顺时针做匀速运动,其上表面的动摩擦因数μ1=0.1,把质量m=20kg的行李包轻放上传送带,释放位置距传送带右端4.5m处.平板车的质量M=30kg,停在传送带的右端,水平地面光滑,行李包与平板车上表面间的动摩擦因数μ2=0.3,平板车长10m,行李包从传送带滑到平板车过程速度不变,行李包可视为质点.(g=10m/s2)求:
如图所示,水平传送带以v=12m/s的速度顺时针做匀速运动,其上表面的动摩擦因数μ1=0.1,把质量m=20kg的行李包轻放上传送带,释放位置距传送带右端4.5m处.平板车的质量M=30kg,停在传送带的右端,水平地面光滑,行李包与平板车上表面间的动摩擦因数μ2=0.3,平板车长10m,行李包从传送带滑到平板车过程速度不变,行李包可视为质点.(g=10m/s2)求:(1)行李包在平板车上相对于平板车滑行的时间是多少?
(2)要想行李包不从平板车滑出,求行李包释放位置应满足什么条件?
分析 (1)先求出行李包滑上小车的速度,滑上小车后,对行李包和小车分别根据牛顿第二定律求出加速度,当速度相等时相对滑动停止;
(2)行李包恰好不从小车右端滑出的位移关系行李包比小车位移多走L,求出滑上小车的临界速度,再根据速度位移关系求出行李包在传送带上的位移;
解答 解:(1)行李包放上传送带做匀加速直线运动.
${a}_{1}^{\;}={μ}_{1}^{\;}g$①
${v}_{\;}^{2}=2{a}_{1}^{\;}x$②
解得v=3m/s<12m/s,符合题意
行李包滑上小车后,行李包减速,小车加速.
${a}_{2}^{\;}={μ}_{2}^{\;}g=3m/{s}_{\;}^{2}$③
${a}_{3}^{\;}=\frac{{μ}_{1}^{\;}mg}{M}=2m/{s}_{\;}^{2}$④
$v-{a}_{2}^{\;}t={a}_{3}^{\;}t$⑤
解得t=0.6s
相对位移s=$vt-\frac{1}{2}{a_2}{t^2}-\frac{1}{2}{a_3}{t^2}=0.9m<10m$,符合题意
(2)当行李包刚好滑到小车右端滑时,行李包与小车相对位移等于车长.设行李包刚滑上传送带时速度为V0,则
${v}_{0}^{\;}-{a}_{2}^{\;}t={a}_{3}^{\;}t$⑥
${v}_{0}^{\;}t-\frac{1}{2}{a}_{2}^{\;}{t}_{\;}^{2}-\frac{1}{2}{a}_{3}^{\;}{t}_{\;}^{2}=L$⑦
解得V0=10m/s<12m/s
行李包在传送带做匀加速直线运动
${v}_{0}^{2}=2{a}_{1}^{\;}x$
解得:x=50m
所以释放位置距离传送带右端应小于50m
答:(1)行李包在平板车上相对于平板车滑行的时间是0.6s;
(2)要想行李包不从平板车滑出,行李包释放位置应满足条件是释放位置距离传送带右端应小于50m
点评 本题考查了牛顿第二定律和运动学公式的应用,解决本题的关键是知道行李包的运动情况,不再发生相对运动的条件是速度相等;第二问要注意理清恰好不滑出的位移关系,灵活运用运动学公式求解.

 阅读快车系列答案
阅读快车系列答案 如图所示,直线MN右测的空间内存在一种匀强场,可能是匀强电场,也可能是匀强磁场.现让一带电粒子(重力忽略不计)从A点以一定速度倾斜穿过直线MN进入右侧区域内.粒子进入边界MN右侧区域后( )
如图所示,直线MN右测的空间内存在一种匀强场,可能是匀强电场,也可能是匀强磁场.现让一带电粒子(重力忽略不计)从A点以一定速度倾斜穿过直线MN进入右侧区域内.粒子进入边界MN右侧区域后( )| A. | 若粒子做曲线运动,则直线MN右侧区域内一定是匀强磁场 | |
| B. | 若粒子做直线运动,则直线MN右侧区域内一定是匀强电场 | |
| C. | 若粒子速度大小不变,则直线MN右侧区域内一定是匀强磁场 | |
| D. | 若粒子又从A点向左穿过直线MN,则直线MN右侧区域内一定是匀强电场 |

假设支架向外伸长的位移为S,弹簧对支架的作用力为恒力,大小为F,支架回到初始位置所用时间为t,我们可以利用惯性质量与引力质量相等原理,则测量者的质量为( )
| A. | $m=\frac{{F{t^2}}}{S}$ | B. | $m=\frac{{F{t^2}}}{2S}$ | C. | $m=\frac{{F{t^2}}}{4S}$ | D. | $m=\frac{Ft}{2S}$ |
 在台秤上,框架内有一轻弹簧,其上端固定在框架顶部,下端系一质量为m的物体,物体下方用竖直细线与框架下部固定,各物体都处于静止状态.今剪断细线,物体开始振动,且框架始终没有离开台秤,弹簧不超出弹性限度,空气阻力忽略不计,重力加速度为g.则下列说法正确的是( )
在台秤上,框架内有一轻弹簧,其上端固定在框架顶部,下端系一质量为m的物体,物体下方用竖直细线与框架下部固定,各物体都处于静止状态.今剪断细线,物体开始振动,且框架始终没有离开台秤,弹簧不超出弹性限度,空气阻力忽略不计,重力加速度为g.则下列说法正确的是( )| A. | 当台秤示数最小时弹簧的长度一定最短 | |
| B. | 当台秤示数最小时物体一定处在平衡位置 | |
| C. | 振动过程中台秤的最大示数一定大于(M+m)g | |
| D. | 振动过程中台秤的最大示数一定等于(M+m)g |
| A. | 布朗运动是指悬浮在液体中的固体小颗粒的无规则热运动 | |
| B. | 清晨荷叶上晶莹剔透的露珠成球形,是水的表面张力作用的结果 | |
| C. | 一定质量的理想气体发生等温变化时,其内能一定不变 | |
| D. | 夏天大气压强要比冬天的低,六月与十一月相比,单位面积上撞击地面的空气分子个数要多 | |
| E. | 干湿泡湿度计的湿泡显示的温度低于干泡显示的温度,这是由于湿泡外纱布中的水蒸发吸热的结果 |
 在X轴上电场方向是水平的,电势随X坐标变化的图象如图2,一个正粒子(不计重力)只受电场力沿X轴从A运动到B的过程.下列说法正确的是( )
在X轴上电场方向是水平的,电势随X坐标变化的图象如图2,一个正粒子(不计重力)只受电场力沿X轴从A运动到B的过程.下列说法正确的是( )| A. | 加速度减小,动能增加 | B. | 加速度减小,动能减小 | ||
| C. | 加速度增加,动能增加 | D. | 加速度增加,动能减小 |

| A. | $\frac{v_0^2}{2μg}$ | B. | v0 t | C. | v0t-$\frac{1}{2}$μgt2 | D. | $\frac{v_0^2}{μg}$ |
 如图所示,在光滑水平面上有一根弹簧固定在墙上,一木块以速度v向右运动,从木块与弹簧接触到弹簧被压缩成最短的过程中,木块所做的运动是( )
如图所示,在光滑水平面上有一根弹簧固定在墙上,一木块以速度v向右运动,从木块与弹簧接触到弹簧被压缩成最短的过程中,木块所做的运动是( )| A. | 加速度增大的变减速运动 | B. | 匀减速运动 | ||
| C. | 加速度减小的变减速运动 | D. | 无法确定 |