题目内容
2. 如图,一半径为R的半圆形轨道竖直固定放置,轨道两端等高;质量为m的质点自轨道端点P由静止开始滑下,滑到最低点Q时,对轨道的正压力为2mg,重力加速度大小为g.质点自P滑到Q的过程中,克服摩擦力所做的功为( )
如图,一半径为R的半圆形轨道竖直固定放置,轨道两端等高;质量为m的质点自轨道端点P由静止开始滑下,滑到最低点Q时,对轨道的正压力为2mg,重力加速度大小为g.质点自P滑到Q的过程中,克服摩擦力所做的功为( )| A. | $\frac{1}{4}$mgR | B. | $\frac{1}{3}$mgR | C. | $\frac{1}{2}$mgR | D. | $\frac{π}{4}$mgR |
分析 质点经过Q点时,由重力和轨道的支持力提供向心力,由牛顿运动定律求出质点经过Q点的速度,再由动能定理求解克服摩擦力所做的功.
解答 解:质点经过Q点时,由重力和轨道的支持力提供向心力,由牛顿第二定律得:
N-mg=m$\frac{{v}_{Q}^{2}}{R}$
由题有:N=2mg
可得:vQ=$\sqrt{gR}$
质点自P滑到Q的过程中,由动能定理得:
mgR-Wf=$\frac{1}{2}m{v}_{Q}^{2}$
得克服摩擦力所做的功为 Wf=$\frac{1}{2}$mgR
故选:C.
点评 本题考查动能定理的应用及向心力公式,要注意正确受力分析,明确指向圆心的合力提供圆周运动的向心力,知道动能定理是求解变力做功常用的方法.

练习册系列答案
相关题目
10. 如图(a),一物块在t=0时刻滑上一固定斜面,其运动的v-t图线如图(b)所示,若重力加速度及图中的v0,v1,t1均为已知量,则可求出( )
如图(a),一物块在t=0时刻滑上一固定斜面,其运动的v-t图线如图(b)所示,若重力加速度及图中的v0,v1,t1均为已知量,则可求出( )
 如图(a),一物块在t=0时刻滑上一固定斜面,其运动的v-t图线如图(b)所示,若重力加速度及图中的v0,v1,t1均为已知量,则可求出( )
如图(a),一物块在t=0时刻滑上一固定斜面,其运动的v-t图线如图(b)所示,若重力加速度及图中的v0,v1,t1均为已知量,则可求出( )| A. | 斜面的倾角 | B. | 物块的质量 | ||
| C. | 物块与斜面间的动摩擦因数 | D. | 物块沿斜面向上滑行的最大高度 |
14. 未来的星际航行中,宇航员长期处于零重力状态,为缓解这种状态带来的不适,有人设想在未来的航天器上加装一段圆柱形“旋转舱”,如图所示,当旋转舱绕其轴线匀速旋转时,宇航员站在旋转舱内圆柱形侧壁上,可以受到与他站在地球表面时相同大小的支持力.为达到上述目的,下列说法正确的是( )
未来的星际航行中,宇航员长期处于零重力状态,为缓解这种状态带来的不适,有人设想在未来的航天器上加装一段圆柱形“旋转舱”,如图所示,当旋转舱绕其轴线匀速旋转时,宇航员站在旋转舱内圆柱形侧壁上,可以受到与他站在地球表面时相同大小的支持力.为达到上述目的,下列说法正确的是( )
 未来的星际航行中,宇航员长期处于零重力状态,为缓解这种状态带来的不适,有人设想在未来的航天器上加装一段圆柱形“旋转舱”,如图所示,当旋转舱绕其轴线匀速旋转时,宇航员站在旋转舱内圆柱形侧壁上,可以受到与他站在地球表面时相同大小的支持力.为达到上述目的,下列说法正确的是( )
未来的星际航行中,宇航员长期处于零重力状态,为缓解这种状态带来的不适,有人设想在未来的航天器上加装一段圆柱形“旋转舱”,如图所示,当旋转舱绕其轴线匀速旋转时,宇航员站在旋转舱内圆柱形侧壁上,可以受到与他站在地球表面时相同大小的支持力.为达到上述目的,下列说法正确的是( )| A. | 旋转舱的半径越大,转动的角速度就应越大 | |
| B. | 旋转舱的半径越大,转动的角速度就应越小 | |
| C. | 宇航员质量越大,旋转舱的角速度就应越大 | |
| D. | 宇航员质量越大,旋转舱的角速度就应越小 |
 如图所示,质量为M0=4kg的木板静止在光滑的水平面上,在木板的右端放置一个质量m=1kg大小可以忽略的铁块,铁块与木板之间的摩擦因数μ=0.4,在铁块上加一个水平向左的恒力F=8N,铁块在长L=6m的木板上滑动.取g=10m/s2.求:
如图所示,质量为M0=4kg的木板静止在光滑的水平面上,在木板的右端放置一个质量m=1kg大小可以忽略的铁块,铁块与木板之间的摩擦因数μ=0.4,在铁块上加一个水平向左的恒力F=8N,铁块在长L=6m的木板上滑动.取g=10m/s2.求: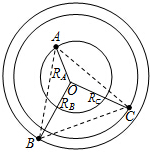 由三颗星体构成的系统,忽略其它星体对它们的作用,存在着一种运动形式:三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O在三角形所在的平面内做相同角速度的圆周运动(图示为A、B、C三颗星体质量不相同时的一般情况).若A星体质量为2m,B、C两星体的质量均为m,三角形的边长为a,求:
由三颗星体构成的系统,忽略其它星体对它们的作用,存在着一种运动形式:三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O在三角形所在的平面内做相同角速度的圆周运动(图示为A、B、C三颗星体质量不相同时的一般情况).若A星体质量为2m,B、C两星体的质量均为m,三角形的边长为a,求:
