题目内容
13.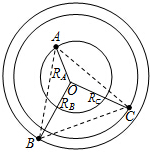 由三颗星体构成的系统,忽略其它星体对它们的作用,存在着一种运动形式:三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O在三角形所在的平面内做相同角速度的圆周运动(图示为A、B、C三颗星体质量不相同时的一般情况).若A星体质量为2m,B、C两星体的质量均为m,三角形的边长为a,求:
由三颗星体构成的系统,忽略其它星体对它们的作用,存在着一种运动形式:三颗星体在相互之间的万有引力作用下,分别位于等边三角形的三个顶点上,绕某一共同的圆心O在三角形所在的平面内做相同角速度的圆周运动(图示为A、B、C三颗星体质量不相同时的一般情况).若A星体质量为2m,B、C两星体的质量均为m,三角形的边长为a,求:(1)A星体所受合力大小FA;
(2)B星体所受合力大小FB;
(3)C星体的轨道半径RC;
(4)三星体做圆周运动的周期T.
分析 (1)(2)由万有引力定律,分别求出单个的力,然后求出合力即可.
(3)C与B的质量相等,所以运行的规律也相等,然后结合向心力的公式即可求出C的轨道半径;
(4)三星体做圆周运动的周期T相等,写出C的向心加速度表达式即可求出.
解答 解:(1)由万有引力定律,A星受到B、C的引力的大小:
${F}_{BA}={F}_{CA}=\frac{G{m}_{A}{m}_{c}}{{a}^{2}}=\frac{G•2{m}^{2}}{{a}^{2}}$
方向如图,则合力的大小为:${F}_{A}=2{F}_{BA}•cos30°=2\sqrt{3}\frac{G{m}^{2}}{{a}^{2}}$
(2)同上,B星受到的引力分别为:${F}_{AB}=\frac{G•2{m}^{2}}{{a}^{2}}$,${F}_{CB}=\frac{G{m}_{B}{m}_{C}}{{a}^{2}}=\frac{G{m}^{2}}{{a}^{2}}$,方向如图;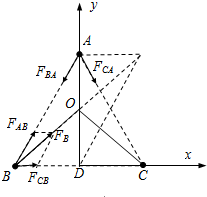
沿x方向:${F}_{Bx}={F}_{AB}•cos60°+{F}_{CB}=2\frac{G{m}^{2}}{{a}^{2}}$
沿y方向:${F}_{By}={F}_{AB}•sin60°=\frac{\sqrt{3}G{m}^{2}}{{a}^{2}}$
可得:${F}_{B}=\sqrt{{F}_{Bx}^{2}+{F}_{By}^{2}}$=$\frac{\sqrt{7}G{m}^{2}}{{a}^{2}}$
(3)通过对于B的受力分析可知,由于:${F}_{AB}=\frac{G•2{m}^{2}}{{a}^{2}}$,${F}_{CB}=\frac{G{m}_{B}{m}_{C}}{{a}^{2}}=\frac{G{m}^{2}}{{a}^{2}}$,合力的方向经过BC的中垂线AD的中点,所以圆心O一定在BC的中垂线AD的中点处.所以:${R}_{C}={R}_{B}=\sqrt{(\frac{1}{2}a)^{2}+(\frac{\sqrt{3}}{4}a)^{2}}=\frac{\sqrt{7}}{4}a$
(4)由题可知C的受力大小与B的受力相同,对C星:${F}_{C}={F}_{B}=\sqrt{7}\frac{G{m}^{2}}{{a}^{2}}=m(\frac{2π}{T})^{2}{R}_{C}$
整理得:$T=π•\sqrt{\frac{{a}^{3}}{Gm}}$
答:(1)A星体所受合力大小是$2\sqrt{3}\frac{G{m}^{2}}{{a}^{2}}$;(2)B星体所受合力大小是$\frac{\sqrt{7}G{m}^{2}}{{a}^{2}}$;(3)C星体的轨道半径是$\frac{\sqrt{7}}{4}a$;(4)三星体做圆周运动的周期T是$π•\sqrt{\frac{{a}^{3}}{Gm}}$.
点评 该题借助于三星模型考查万有引力定律,其中B与C的质量相等,则运行的规律、运动的半径是相等的.画出它们的受力的图象,在结合图象和万有引力定律即可正确解答.

 53随堂测系列答案
53随堂测系列答案 如图所示,单匝圆形线框中磁场正均匀变化,其磁感应强度随时间的变化关系已经在乙图标出,已知圆形线框面积为0.2m2,内阻r=1Ω,定值电阻R=1Ω,电表均为理想电表,其余电阻不计,以垂直纸面向外为磁感应强度正方形,则以下判断正确的是( )
如图所示,单匝圆形线框中磁场正均匀变化,其磁感应强度随时间的变化关系已经在乙图标出,已知圆形线框面积为0.2m2,内阻r=1Ω,定值电阻R=1Ω,电表均为理想电表,其余电阻不计,以垂直纸面向外为磁感应强度正方形,则以下判断正确的是( )| A. | 圆形线框中感应电流方向始终为逆时针 | |
| B. | 线框始终有扩张的趋势 | |
| C. | 电压表示数为1V | |
| D. | 电流表示数为0.02A |
 如图,直线a、b和c、d是处于匀强电场中的两组平行线,M、N、P、Q是它们的交点,四点处的电势分别为φM,φN,φP,φQ,一电子由M点分别到N点和P点的过程中,电场力所做的负功相等,则( )
如图,直线a、b和c、d是处于匀强电场中的两组平行线,M、N、P、Q是它们的交点,四点处的电势分别为φM,φN,φP,φQ,一电子由M点分别到N点和P点的过程中,电场力所做的负功相等,则( )| A. | 直线a位于某一等势面内,φM>φQ | |
| B. | 直线c位于某一等势面内,φM>φN | |
| C. | 若电子由M点运动到Q点,电场力做正功 | |
| D. | 若电子由P点运动到Q点,电场力做负功 |
 如图,一半径为R的半圆形轨道竖直固定放置,轨道两端等高;质量为m的质点自轨道端点P由静止开始滑下,滑到最低点Q时,对轨道的正压力为2mg,重力加速度大小为g.质点自P滑到Q的过程中,克服摩擦力所做的功为( )
如图,一半径为R的半圆形轨道竖直固定放置,轨道两端等高;质量为m的质点自轨道端点P由静止开始滑下,滑到最低点Q时,对轨道的正压力为2mg,重力加速度大小为g.质点自P滑到Q的过程中,克服摩擦力所做的功为( )| A. | $\frac{1}{4}$mgR | B. | $\frac{1}{3}$mgR | C. | $\frac{1}{2}$mgR | D. | $\frac{π}{4}$mgR |
 轻质弹簧上端固定,下端连接质量m=3kg的物块A,物块A放在平台B上,通过平台B可以控制A的运动,如图所示.初始时A、B静止,弹簧处于原长.已知弹簧的劲度系数k=200N/m,g=10m/s2.(计算结果保留两位有效数字)
轻质弹簧上端固定,下端连接质量m=3kg的物块A,物块A放在平台B上,通过平台B可以控制A的运动,如图所示.初始时A、B静止,弹簧处于原长.已知弹簧的劲度系数k=200N/m,g=10m/s2.(计算结果保留两位有效数字)
