题目内容
11.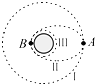 我国月球探测活动的第一步“绕月”工程和第二步“落月”工程已按计划在2013年以前顺利完成.假设月球半径为R,月球表面的重力加速度为g0,飞船沿距月球表面高度为3R的圆形轨道Ⅰ运动,到达轨道的A点时点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B时再次点火进入月球近月轨道Ⅲ绕月球做圆周运动,下列判断正确的是( )
我国月球探测活动的第一步“绕月”工程和第二步“落月”工程已按计划在2013年以前顺利完成.假设月球半径为R,月球表面的重力加速度为g0,飞船沿距月球表面高度为3R的圆形轨道Ⅰ运动,到达轨道的A点时点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B时再次点火进入月球近月轨道Ⅲ绕月球做圆周运动,下列判断正确的是( )| A. | 飞船在在轨道Ⅰ上的速度大于轨道Ⅲ的速度 | |
| B. | 飞船在椭圆轨道Ⅱ上从A到B运行的过程中机械能增大 | |
| C. | 飞船在轨道Ⅲ绕月球运动一周所需的时间T=π$\sqrt{\frac{R}{{g}_{0}}}$ | |
| D. | 飞船在轨道Ⅰ上的运行速率v=$\frac{\sqrt{{g}_{0}R}}{2}$ |
分析 在月球表面,万有引力等于重力,在任意轨道,万有引力提供向心力,联立方程即可求解,卫星变轨也就是近心运动或离心运动,根据提供的万有引力和所需的向心力关系确定.飞船在近月轨道Ⅲ绕月球运行,重力提供向心力,根据向心力周期公式即可求解.
解答 解:A、据万有引力提供圆周运动向心力$G\frac{mM}{{r}^{2}}=m\frac{{v}^{2}}{r}$可得v=$\sqrt{\frac{GM}{r}}$,可得卫星的轨道半径大线速度小,故A错误;
B、飞船从A到B的过程中,只有万有引力做功,机械能守恒不变,故B错误;
C、在月球表面有:$G\frac{mM}{{R}^{2}}=m{g}_{0}$,在轨道III上运动有:$G\frac{mM}{{R}^{2}}=mR(\frac{2π}{T})^{2}$联列方程可得:卫星在轨道III上运动一周所需时间T=$2π\sqrt{\frac{{g}_{0}}{R}}$,故C错误;
D、在月球表面有$G\frac{mM}{{R}^{2}}=m{g}_{0}$,在轨道I上运动有:$G\frac{mM}{(R+3R)^{2}}=m\frac{{v}^{2}}{R+3R}$,解得v=$\frac{\sqrt{{g}_{0}R}}{2}$,故D正确.
故选:D.
点评 解决本题的关键掌握万有引力定律的两个重要理论:1、万有引力提供向心力,2、万有引力等于重力,并能灵活运用.

练习册系列答案
相关题目
2.下列电器设备的工作原理中不涉及到电磁感应的是( )
| A. | 灵敏电流计 | B. | 电磁炉 | C. | 日光灯 | D. | 动圈式话筒 |
19.跳伞表演是观赏性很强体育项目.当运动员从直升飞机由静止跳下后,在下落过程中会受到水平风力的影响.下列说法中正确的是( )
| A. | 风力越大,运动员下落时间越短 | B. | 风力越大,运动员着地速度越小 | ||
| C. | 运动员下落时间与风力无关 | D. | 运动员着地速度与风力无关 |
16. 一质量为m的物体以某一速度从固定斜面底端冲上倾角α=30°的斜面,其加速度为$\frac{3}{4}$g,如图所示,物体在斜面上上升的最大高度为h,则此过程中正确的是( )
一质量为m的物体以某一速度从固定斜面底端冲上倾角α=30°的斜面,其加速度为$\frac{3}{4}$g,如图所示,物体在斜面上上升的最大高度为h,则此过程中正确的是( )
 一质量为m的物体以某一速度从固定斜面底端冲上倾角α=30°的斜面,其加速度为$\frac{3}{4}$g,如图所示,物体在斜面上上升的最大高度为h,则此过程中正确的是( )
一质量为m的物体以某一速度从固定斜面底端冲上倾角α=30°的斜面,其加速度为$\frac{3}{4}$g,如图所示,物体在斜面上上升的最大高度为h,则此过程中正确的是( )| A. | 动能减小了$\frac{3}{4}$mgh | B. | 重力势能减少了mgh | ||
| C. | 机械能损失了$\frac{1}{2}$mgh | D. | 物体克服摩擦力做功$\frac{1}{4}$mgh |
 在测定玻璃砖折射率的实验中:
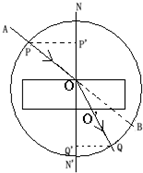
在测定玻璃砖折射率的实验中: 普通照像机爆光$\frac{1}{50}$s拍摄一幅相片.由于小球落下有速度,则对下落着的小球拍摄相片均不是球型,而是“长圆”形,如图所示,下落速度越大,拍摄相片越长.设小球直径1cm,当小球刚下落立即拍片,其像长约为1.2cm,当小球下落时间更长才开拍相片,像的长度就更长.由此可知研究自由落体一定要用频闪照相机,你知道频闪照相机的特点是什么?
普通照像机爆光$\frac{1}{50}$s拍摄一幅相片.由于小球落下有速度,则对下落着的小球拍摄相片均不是球型,而是“长圆”形,如图所示,下落速度越大,拍摄相片越长.设小球直径1cm,当小球刚下落立即拍片,其像长约为1.2cm,当小球下落时间更长才开拍相片,像的长度就更长.由此可知研究自由落体一定要用频闪照相机,你知道频闪照相机的特点是什么?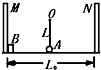 如图,绳长L=0.1m.质量为m=0.01Kg的小球和水平面接触但无相互作用,球两侧等距处放有固定挡板M、N,MN=L0=2m.现有一质量也为m=0.01Kg的小物体B靠在M挡板处,它与水平面间的摩擦因数μ=0.25.物体与小球连线垂直于挡板M、N和绳.现物体B以初速V=10m/s从挡板M处向小球A运动.物体与小球碰撞时速度变为零,小球获得物体碰前的速度,物体与挡板碰撞将以相同速率反弹回来.物体和小球均可看成质点,那么物体和小球第一次碰撞后瞬间,细绳对小球的拉力为9.6 N;物体从开始运动至最后停止的过程中,小球共转了10个整圈.(g=10m/s2)
如图,绳长L=0.1m.质量为m=0.01Kg的小球和水平面接触但无相互作用,球两侧等距处放有固定挡板M、N,MN=L0=2m.现有一质量也为m=0.01Kg的小物体B靠在M挡板处,它与水平面间的摩擦因数μ=0.25.物体与小球连线垂直于挡板M、N和绳.现物体B以初速V=10m/s从挡板M处向小球A运动.物体与小球碰撞时速度变为零,小球获得物体碰前的速度,物体与挡板碰撞将以相同速率反弹回来.物体和小球均可看成质点,那么物体和小球第一次碰撞后瞬间,细绳对小球的拉力为9.6 N;物体从开始运动至最后停止的过程中,小球共转了10个整圈.(g=10m/s2)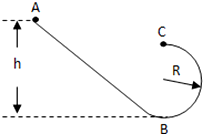 如图所示,竖直平面内的轨道由轨道AB和圆弧轨道BC组成,小球从斜面上A点由静止开始滑下,滑到斜面底端后又滑上一个半径为R的圆轨道,
如图所示,竖直平面内的轨道由轨道AB和圆弧轨道BC组成,小球从斜面上A点由静止开始滑下,滑到斜面底端后又滑上一个半径为R的圆轨道,