题目内容
如图所示，在光滑桌面上放着长木板，其长度为L=1.0m，在长木板的左上端放一可视为质点的小金属块，它的质量和木板的质量相等，最初它们是静止的．现让小金属块以v=2.0m/s的初速度开始向右滑动，当滑动到长木板的右端时，滑块的速度为v1=1.0m/s，取 g=l0m/s2，求：（1）小金属块刚滑到长木板右端时的速度大小v2及滑块与长木板间的动摩擦因数μ；
（2）小金属块刚滑到长木板右端时经历的时间t及长木板的位移大小x．
【答案】分析：由动量守恒定律与能量守恒定律可以求出金属块速度与动摩擦因数．
应用动能定理可以求出木板的位移，由牛顿第二定律与运动学公式可以求出运动时间．
解答：解：（1）设小金属块和木板的质量均为m，
以小金属块与木板组成的系统为研究对象，
由动量守恒定律可得：mv=mvl+mv2，
由能量守恒定律可得：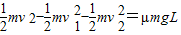
，
解得：v2=1 m/s，μ=0.1；
（2）对木板由动能定理得：μmgx=
mv22-0，解得x=0.5m；
对木板，由牛顿第二定律得：μmg=ma，
由匀变速运动的速度公式得：v2=at，解得：t=1s；
答：（1）小金属块刚滑到长木板右端时的速度为1m/s，滑块与长木板间的动摩擦因数为0.1．
（2）小金属块刚滑到长木板右端时经历的时间为1s，长木板的位移大小为0.5m．
点评：该题满足动量守恒定律的条件，直接代入动量守恒公式即可解得结果．属于常规题目，难度不大．
应用动能定理可以求出木板的位移，由牛顿第二定律与运动学公式可以求出运动时间．
解答：解：（1）设小金属块和木板的质量均为m，
以小金属块与木板组成的系统为研究对象，
由动量守恒定律可得：mv=mvl+mv2，
由能量守恒定律可得：
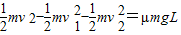，解得：v2=1 m/s，μ=0.1；
（2）对木板由动能定理得：μmgx=
mv22-0，解得x=0.5m；对木板，由牛顿第二定律得：μmg=ma，
由匀变速运动的速度公式得：v2=at，解得：t=1s；
答：（1）小金属块刚滑到长木板右端时的速度为1m/s，滑块与长木板间的动摩擦因数为0.1．
（2）小金属块刚滑到长木板右端时经历的时间为1s，长木板的位移大小为0.5m．
点评：该题满足动量守恒定律的条件，直接代入动量守恒公式即可解得结果．属于常规题目，难度不大．
练习册系列答案
相关题目
如图所示，在光滑桌面上放着长木板，其长度为L=1.0m，在长木板的左上端放一可视为质点的小金属块，它的质量和木板的质量相等，最初它们是静止的．现让小金属块以v0=2.0m/s的初速度开始向右滑动，当滑动到长木板的右端时，滑块的速度为v1=1.0m/s，取 g=l0m/s2，求：
如图所示，在光滑桌面上并排放着质量分别为m、M的两个物体，对m施加一个水平推力F，则它们一起向右作匀加速直线运动，其加速度大小为
（1）以下是有关近代物理内容的若干叙述，其中正确的是
如图所示，在光滑桌面上放着两个完全相同的木板A和B，它们靠拢但并不相连，长度皆为L=1.0m，在木板A的左上端放一可视为质点的小金属块，它的质量和木板的质量相等，金属块与木板间的动摩擦因数μ=0.10，最初它们是静止的．现让小金属块以V0=2.0m/s的初速度开始向右滑动，取 g=l0m/s2，求：