Question

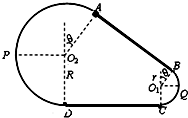（2011?浙江模拟）如图所示为放置在竖直平面内游戏滑轨的模拟装置，滑轨由四部分粗细均匀的金属杆组成，其中倾斜直轨AB与水平直轨CD长均为L=3m，圆弧形轨道APD和BQC均光滑，BQC的半径为r=1m，APD的半径为R，AB、CD与两圆弧形轨道相切，O₂A、O₁B与竖直方向的夹角均为θ=37⁰．现有一质量为m=1kg的小环穿在滑轨上，以某一初速度从B点开始沿AB向上运动，并恰能通过滑轨最高点．设小环与两段直轨道间的动摩擦因数均为μ=

1

3

，经过轨道连接
处均无能量损失．（g=

10m

s2

，sin37°=0.6，cos37°=0.8，sin18.5°=0.32，cos18.5°=0.95，tan18.5°=

1

3

，cot18.5°=3）求：
（1）小球的初速度v₀；
（2）小球第一次到达圆弧C点时对轨道的压力；
（3）小球最后停在何处．

Answer 1

分析：从图形中几何关系找出APD的半径为R．
运用动能定理研究小球圆弧的最高点到第一次到轨道上C点求出C点速度．
小球在C点进行受力分析运用牛顿第二定律求解．

解答：解：（1）R=Ltan18.5°+r=2m
（或R+R?cos37°=r+rcos37°+L?sin37°）
解得：R=2m
要使小球过大圆弧的最高点，到达圆弧的最高点的临界速度为0．
运用动能定理研究从B点到圆弧的最高点：
0-

1

2

m

v

2 0

=-mgR(1-cosθ)-mgLsinθ-μmgLcosθ
代入数据解得v0=2

15

m/s
（2）运用动能定理研究小球圆弧的最高点到第一次到轨道上C点：
mg2R-μmgL=

1

2

m

v

2 c

小球在C点进行受力分析运用牛顿第二定律得：
FN-mg=m

v 2 c

r

代入数据解得F_N=7mg=70N
由牛顿第三定律得：对轨道的压力F'_N=70N，
（3）由第一问分析可知，小球再次到达B点时还有动能，设小球沿AB向上运动的位移为s
则有：

1

2

m

v

2 0

=μmgcosθ(L+s)+μmgL+mgssinθ
代入数据解得s=

18

13

m=1.38m
小球继续向下运动，到B点时的动能为E_KB=E_K0-μmgcosθ（L+2s）-μmgL
代入解得E_KB=4.6J
因E_KB＜2μmgL，故小球无法继续上升到B点，滑到BQC某处后开始下滑，之后受摩擦力作用，小球最终停在CD上的某点．
由动能定理：E_kc=μmgx
解得：x=0.78m
小球最后停在C点左侧距C点0.78m处．
答：（1）小球的初速度v₀为2

15

m/s；
（2）小球第一次到达圆弧C点时对轨道的压力是70N；
（3）小球最后停在C点左侧距C点0.78m处．

点评：一个题目可能需要选择不同的过程多次运用动能定理研究．
圆周运动问题关键要通过受力分析找出向心力的来源列出等式解决问题．