题目内容
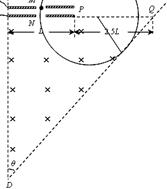
如图所示,两块平行板电极的长度为L,两板间距离远小于L,可忽略不计。两板的正中央各有一个小孔M、N,两孔连线与板垂直。现将两极板分别接在可调直流电压U的两端,极板处在一有界匀强磁场(板内无磁场),磁感应强度为B,磁场的两条边界CD、DE的夹角θ=60°。下极板延长线与边界DE交于Q点,极板最右端P与Q间距离为2.5L。现将比荷均为![]() 的各种粒子分别从M孔射入电场,不考虑粒子的重力。将带正电的粒子从M无初速释放,
的各种粒子分别从M孔射入电场,不考虑粒子的重力。将带正电的粒子从M无初速释放,
①若粒子恰好打到下极板右端,求所加直流电压的值U1.
②若![]() ,则该粒子经过多少次电场的加速后可以离开磁场区域?
,则该粒子经过多少次电场的加速后可以离开磁场区域?

解:
①若粒子刚好打到下板的右端,则由几何关系得![]() ,即
,即![]() 2分
2分
由![]() 2分
2分
得![]() 1分
1分
又![]() 2分
2分
解得![]() 1分
1分
②假设粒子经过n次电场加速后的速度为![]() ,此时粒子轨迹恰好能与ED边界相切,如图,轨迹半径为
,此时粒子轨迹恰好能与ED边界相切,如图,轨迹半径为![]() 。由几何关系得
。由几何关系得 ![]() 2分
2分
解得![]() 2分
2分
又![]() 2分
2分
又粒子被电场加速n次,则![]() 2分
2分
代入解得n=2.25 1分
即粒子经过三次电场加速后离开磁场区域。 1分

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
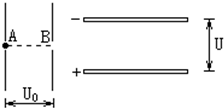 如图所示为两组平行板金属板,一组竖直放置,一组水平放置,今有一质量为m的电子静止在竖直放置的平行金属板的A点,经电压U0加速后通过B点进入两板间距为d、电压为U的水平放置的平行金属板间,若电子从两块水平平行板的正中间射入,且最后电子刚好能从右侧的两块平行金属板穿出,A、B分别为两块竖直板的中点,求:
如图所示为两组平行板金属板,一组竖直放置,一组水平放置,今有一质量为m的电子静止在竖直放置的平行金属板的A点,经电压U0加速后通过B点进入两板间距为d、电压为U的水平放置的平行金属板间,若电子从两块水平平行板的正中间射入,且最后电子刚好能从右侧的两块平行金属板穿出,A、B分别为两块竖直板的中点,求: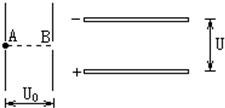 如图所示为两组平行板金属板,一组竖直放置,一组水平放置,今有一质量为m的电量为e的电子静止在竖直放置的平行金属板的A点,经电压U0加速后通过B点进入两板间距为d、电压为U的水平放置的平行金属板间,若电子从两块水平平行板的正中间射入,且最后电子刚好能从右侧的两块平行金属板穿出,A、B分别为两块竖直板的中点,求:
如图所示为两组平行板金属板,一组竖直放置,一组水平放置,今有一质量为m的电量为e的电子静止在竖直放置的平行金属板的A点,经电压U0加速后通过B点进入两板间距为d、电压为U的水平放置的平行金属板间,若电子从两块水平平行板的正中间射入,且最后电子刚好能从右侧的两块平行金属板穿出,A、B分别为两块竖直板的中点,求:
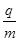 的各种粒子分别从M孔射入电场,不考虑粒子的重力。将带正电的粒子从M无初速释放,
的各种粒子分别从M孔射入电场,不考虑粒子的重力。将带正电的粒子从M无初速释放,
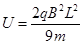 ,则该粒子经过多少次电场的加速后可以离开磁场区域?
,则该粒子经过多少次电场的加速后可以离开磁场区域?