题目内容
13. 如图所示,A船从港口P出发去拦截正以速度uo沿直线匀速航行的船B,P与B所在航线的垂直距离为a,A船起航时,B船与P的距离为b(b>a),若忽略A船启动时间,认为它一起航就匀速运动,则A船能拦截到B船所需的最小速率为( )
如图所示,A船从港口P出发去拦截正以速度uo沿直线匀速航行的船B,P与B所在航线的垂直距离为a,A船起航时,B船与P的距离为b(b>a),若忽略A船启动时间,认为它一起航就匀速运动,则A船能拦截到B船所需的最小速率为( )| A. | υ0 | B. | $\frac{a}{b}$v0 | C. | $\frac{b}{a}$v0 | D. | $\frac{a}{\sqrt{{b}^{2}-{a}^{2}}}$v0 |
分析 对A的速度沿MN和PN的方向进行正交分解,利用等时性在MN和PN的方向上列式,通过数学知识的推导,即可得知A船能拦截到B船的最小速度.
解答 解:对B船的速度沿MN和PN的方向进行正交分解为vx和vy,有运动的等时性有:$\frac{a}{{v}_{y}}$=$\frac{\sqrt{{b}^{2}-{a}^{2}}}{{v}_{0}-{v}_{x}}$
得:vy=$\frac{a({v}_{0}{v}_{x})}{\sqrt{{b}^{2}-{a}^{2}}}$ …①
A船的速度为:
v=$\sqrt{{v}_{x}^{2}+{v}_{y}^{2}}$ …②
折MN的长度为c,有:b2-a2=c2…③
将①式代入②式并结合③式得:
v=$\sqrt{\frac{(b{v}_{x}-\frac{{a}^{2}{v}_{0}}{b})^{2}}{{c}^{2}}+\frac{{a}^{2}{v}_{0}^{2}}{{b}^{2}}}$
当且仅当bvx=$\frac{{a}^{2}{v}_{0}}{b}$ 时,v有最小值,为:
v=$\frac{a{v}_{0}}{b}$,故ACD错误,B正确;
故选:B.
点评 该题是一道非常容易出错的一道题,往往会认为A船沿PN的方向航行,速度最小.解答该题的关键是把A船的速度进行正交分解后,根据数学知识列式并推导出A的速度的表达式,结合数学知识判断A船的速度由极值的条件,继而可得A船的最小速度.该题还可利用相对运动的知识求解,以B为参考系,A相对于B的运动就是沿PM方向做匀速直线运动,也可得知A船最小速度.

练习册系列答案
相关题目
3. 如图所示,在同一平面内,大小分别为1N、2N、3N、4N、5N、6N的六个力共同作用于一点,其合力大小为( )
如图所示,在同一平面内,大小分别为1N、2N、3N、4N、5N、6N的六个力共同作用于一点,其合力大小为( )
 如图所示,在同一平面内,大小分别为1N、2N、3N、4N、5N、6N的六个力共同作用于一点,其合力大小为( )
如图所示,在同一平面内,大小分别为1N、2N、3N、4N、5N、6N的六个力共同作用于一点,其合力大小为( )| A. | 1N | B. | 0 | C. | 2N | D. | 3N |
4. 利用电动机通过如图所示的电路提升重物,已知电源电动势E,电源内阻r,电动机内电阻R,其他部分的电阻不计.闭合开关,电动机正常工作时,电路中的电流为I,路端电压为U,则下列说法正确的是( )
利用电动机通过如图所示的电路提升重物,已知电源电动势E,电源内阻r,电动机内电阻R,其他部分的电阻不计.闭合开关,电动机正常工作时,电路中的电流为I,路端电压为U,则下列说法正确的是( )
 利用电动机通过如图所示的电路提升重物,已知电源电动势E,电源内阻r,电动机内电阻R,其他部分的电阻不计.闭合开关,电动机正常工作时,电路中的电流为I,路端电压为U,则下列说法正确的是( )
利用电动机通过如图所示的电路提升重物,已知电源电动势E,电源内阻r,电动机内电阻R,其他部分的电阻不计.闭合开关,电动机正常工作时,电路中的电流为I,路端电压为U,则下列说法正确的是( )| A. | 路端电压U等于IR | |
| B. | 电动机提升重物做功的功率为P=UI-I2R | |
| C. | 电源的总功率为P总=$\frac{E^2}{R+r}$ | |
| D. | 电源的效率为η=$\frac{U}{E}$×100% |
1.在如图电路中,当滑动变阻器滑动键P向上移动时,则( )
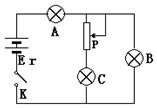

| A. | A灯变亮、B灯变暗、C灯变亮 | B. | A灯变暗、B灯变暗、C灯变亮 | ||
| C. | A灯变亮、B灯变暗、C灯变暗 | D. | A灯变暗、B灯变亮、C灯变暗 |
8. 如图所示,有一个半径为R的光滑圆轨道,现给小球一个初速度,使小球在竖直面内做圆周运动,则关于小球在过最高点的速度v,下列叙述中正确的是( )
如图所示,有一个半径为R的光滑圆轨道,现给小球一个初速度,使小球在竖直面内做圆周运动,则关于小球在过最高点的速度v,下列叙述中正确的是( )
 如图所示,有一个半径为R的光滑圆轨道,现给小球一个初速度,使小球在竖直面内做圆周运动,则关于小球在过最高点的速度v,下列叙述中正确的是( )
如图所示,有一个半径为R的光滑圆轨道,现给小球一个初速度,使小球在竖直面内做圆周运动,则关于小球在过最高点的速度v,下列叙述中正确的是( )| A. | v的最小值为0 | |
| B. | v由零逐渐增大,轨道对球的弹力逐渐增大 | |
| C. | 当v由$\sqrt{gR}$值逐渐增大时,轨道对小球的弹力也逐渐增大 | |
| D. | 当v由$\sqrt{gR}$值逐渐减小时,轨道对小球的弹力也逐渐增大 |
18.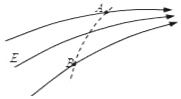 某电场的部分电场线如图所示,A、B是一带电粒子仅在电场力作用下运动轨迹(图中虚线)上的两点,下列说法中正确的是( )
某电场的部分电场线如图所示,A、B是一带电粒子仅在电场力作用下运动轨迹(图中虚线)上的两点,下列说法中正确的是( )
 某电场的部分电场线如图所示,A、B是一带电粒子仅在电场力作用下运动轨迹(图中虚线)上的两点,下列说法中正确的是( )
某电场的部分电场线如图所示,A、B是一带电粒子仅在电场力作用下运动轨迹(图中虚线)上的两点,下列说法中正确的是( )| A. | 带点粒子带负电 | |
| B. | 粒子一定是从B点向A点运动 | |
| C. | 电场中A点的电势高于B点的电势 | |
| D. | 粒子在A点的加速度大于它在B点的加速度 |
5.下列说法正确的是( )
| A. | 划船时浆向后推水,水就向前推浆,因为水推浆的力大于浆推水的力,船才被推着前进 | |
| B. | 完全失重的物体将不受到重力,所以此刻一切由重力引起的现象都将消失 | |
| C. | 人在沿直线加速前进的车厢内,竖直向上跳起后,将落在起跳点的后方 | |
| D. | 物体的运动与外界的推、拉等行为相联系,如果不再推、拉,原来的运动将停下来这说明必须有力作用,物体才能运动 |
3. 如图所示,小孩用与水平方向成θ角的轻绳拉放在水平面上的箱子,第一次轻拉,没有拉动;第二次用更大的力拉(拉力方向不变),箱子还是不动,则( )
如图所示,小孩用与水平方向成θ角的轻绳拉放在水平面上的箱子,第一次轻拉,没有拉动;第二次用更大的力拉(拉力方向不变),箱子还是不动,则( )
 如图所示,小孩用与水平方向成θ角的轻绳拉放在水平面上的箱子,第一次轻拉,没有拉动;第二次用更大的力拉(拉力方向不变),箱子还是不动,则( )
如图所示,小孩用与水平方向成θ角的轻绳拉放在水平面上的箱子,第一次轻拉,没有拉动;第二次用更大的力拉(拉力方向不变),箱子还是不动,则( )| A. | 第二次拉时箱子受支持力减小 | B. | 第二次拉时箱子受支持力增大 | ||
| C. | 第二次拉时箱子受摩擦力不变 | D. | 第二次拉时箱子受摩擦力减小 |