题目内容
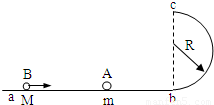 如图所示,abc是光滑的轨道,其中ab是水平的,bc为与ab相切的位于竖直平面内的半圆,半径R=0.30m.质量m=0.20kg的小球A静止在轨道上,另一质量M=0.60kg、速度V=5.5m/s的小球B与小球A正碰.已知相碰后小球A经过半圆的最高点c落到轨道上距b点为L=4R处,重力加速度g取10m/s2,求:
如图所示,abc是光滑的轨道,其中ab是水平的,bc为与ab相切的位于竖直平面内的半圆,半径R=0.30m.质量m=0.20kg的小球A静止在轨道上,另一质量M=0.60kg、速度V=5.5m/s的小球B与小球A正碰.已知相碰后小球A经过半圆的最高点c落到轨道上距b点为L=4R处,重力加速度g取10m/s2,求:(1)碰撞结束时,小球A和B的速度大小;
(2)试论证小球B是否能沿着半圆轨道到达c点?
【答案】分析:(1)根据平抛运动的规律,求出A球在C点的速度,根据机械能守恒定律求出A球碰后的速度,根据动量守恒定律求出B球碰后的速度.
(2)根据机械能守恒定律求出B球到底最高点的速度,再根据牛顿第二定律求出最高点的最小速度,然后进行比较,判断能否到达最高点.
解答:解:(1)分别以v1和v2表示小球A和B碰后的速度,v3表示小球A在半圆最高点的速度,则对A由平抛运动规律有:L=v3t
h=2R=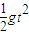
解得:v3=2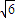 m/s.
m/s.
对A运用机械能守恒定律得: mv12=2mgR+
mv12=2mgR+ mv32
mv32
以A和B为系统,碰撞前后动量守恒:Mv=Mv2+mv1
联立解得:v1=6m/s,v2=3.5m/s.
(2)小球B刚能沿着半圆轨道上升到最高点的条件是在最高点弹力为零、重力作为向心力,故有:Mg=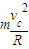
由机械能守恒定律有: MVB2=2RMg+
MVB2=2RMg+ Mvc2
Mvc2
解得:vB=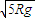 =3.9m/s>v2,可知小球B不能达到半圆轨道的最高点.
=3.9m/s>v2,可知小球B不能达到半圆轨道的最高点.
答:(1)碰撞结束时,小球A和B的速度大小分别为6m/s、3.5m/s.
(2)小球B不能达到半圆轨道的最高点.
点评:本题考查了动量守恒定律、机械能守恒定律、牛顿第二定律等规律,综合性较强,需在平时的学习中加强训练.
(2)根据机械能守恒定律求出B球到底最高点的速度,再根据牛顿第二定律求出最高点的最小速度,然后进行比较,判断能否到达最高点.
解答:解:(1)分别以v1和v2表示小球A和B碰后的速度,v3表示小球A在半圆最高点的速度,则对A由平抛运动规律有:L=v3t
h=2R=
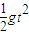
解得:v3=2
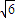 m/s.
m/s.对A运用机械能守恒定律得:
 mv12=2mgR+
mv12=2mgR+ mv32
mv32 以A和B为系统,碰撞前后动量守恒:Mv=Mv2+mv1
联立解得:v1=6m/s,v2=3.5m/s.
(2)小球B刚能沿着半圆轨道上升到最高点的条件是在最高点弹力为零、重力作为向心力,故有:Mg=
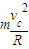
由机械能守恒定律有:
 MVB2=2RMg+
MVB2=2RMg+ Mvc2
Mvc2 解得:vB=
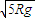 =3.9m/s>v2,可知小球B不能达到半圆轨道的最高点.
=3.9m/s>v2,可知小球B不能达到半圆轨道的最高点.答:(1)碰撞结束时,小球A和B的速度大小分别为6m/s、3.5m/s.
(2)小球B不能达到半圆轨道的最高点.
点评:本题考查了动量守恒定律、机械能守恒定律、牛顿第二定律等规律,综合性较强,需在平时的学习中加强训练.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
 如图所示,ABC是一个透明的薄壁容器,内装液体,当光垂直射向AC面时,光在AB面恰好发生全反射,已知光在真空中的传播速度为c,求液体的折射率及光在该液体中传播速度多大?
如图所示,ABC是一个透明的薄壁容器,内装液体,当光垂直射向AC面时,光在AB面恰好发生全反射,已知光在真空中的传播速度为c,求液体的折射率及光在该液体中传播速度多大? (2006?南通一模)如图所示,ABC是由折射率为
(2006?南通一模)如图所示,ABC是由折射率为 如图所示,ABC是由折射率为
如图所示,ABC是由折射率为 如图所示,ABC是三棱镜的一个截面,其折射率为n=1.5.现有一细束平行于截面的光线沿MN方向射到棱镜的AB面上的N点,AN=NB=2cm,入射角的大小为i,且sini=0.75.已知真空中的光速c=3.0×108m/s,求:
如图所示,ABC是三棱镜的一个截面,其折射率为n=1.5.现有一细束平行于截面的光线沿MN方向射到棱镜的AB面上的N点,AN=NB=2cm,入射角的大小为i,且sini=0.75.已知真空中的光速c=3.0×108m/s,求: