题目内容
固定于竖直面内的粗糙斜杆,在水平方向夹角为30,质量为m的小球套在杆上,在大小不变的拉力作用下,小球沿杆由底端匀速运动到顶端,为使拉力做功最小,拉力F与杆的夹角α和拉力大小F各为多少( )A.α=0°,F=
 mg
mgB.α=45°,F=
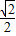 mg
mgC.α=60°,F=
 mg
mgD.α=60°,F=mg
【答案】分析:明确动能定理中功的含义是各力做功的代数和,小球匀速的含义是小球所受的合力是零.
解答:解:小球由底端到顶端过程由动能定理得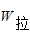 +
+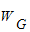
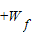 =
=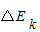 =0,可知,若要求拉力做功最小应使摩擦力做功
=0,可知,若要求拉力做功最小应使摩擦力做功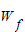 为零,即f=0,由f=μ
为零,即f=0,由f=μ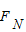 得
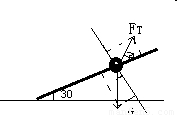
得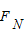 =0,对小球受力分析如图,设拉力方向与杆夹角为α,由平衡条件得
=0,对小球受力分析如图,设拉力方向与杆夹角为α,由平衡条件得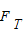 .cosα=mgsin30°,
.cosα=mgsin30°,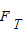 sinα=mgcos30°,两式联立可解得α=60°,F=mg,故D正确,ABC错误.
sinα=mgcos30°,两式联立可解得α=60°,F=mg,故D正确,ABC错误.
故选D.
点评:本题因滑动摩擦力球运动方向相反,故若摩擦力不做功,即摩擦力因为零,由f=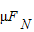 知,则弹力一定是零.
知,则弹力一定是零.
解答:解:小球由底端到顶端过程由动能定理得
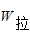 +
+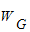
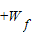 =
=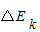 =0,可知,若要求拉力做功最小应使摩擦力做功
=0,可知,若要求拉力做功最小应使摩擦力做功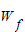 为零,即f=0,由f=μ
为零,即f=0,由f=μ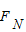 得
得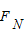 =0,对小球受力分析如图,设拉力方向与杆夹角为α,由平衡条件得
=0,对小球受力分析如图,设拉力方向与杆夹角为α,由平衡条件得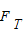 .cosα=mgsin30°,
.cosα=mgsin30°,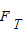 sinα=mgcos30°,两式联立可解得α=60°,F=mg,故D正确,ABC错误.
sinα=mgcos30°,两式联立可解得α=60°,F=mg,故D正确,ABC错误.
故选D.
点评:本题因滑动摩擦力球运动方向相反,故若摩擦力不做功,即摩擦力因为零,由f=
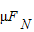 知,则弹力一定是零.
知,则弹力一定是零. 
练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
 如图,固定于竖直面内的粗糙斜杆,与水平方向夹角为30°,质量为m=1kg的小球套在杆上,小球与杆间动摩擦因数为μ=
如图,固定于竖直面内的粗糙斜杆,与水平方向夹角为30°,质量为m=1kg的小球套在杆上,小球与杆间动摩擦因数为μ=
 如图,固定于竖直面内的粗糙斜杆,在水平方向夹角为30°,质量为m的小球套在杆上,在大小不变的拉力作用下,小球沿杆由底端匀速运动到顶端,为使拉力做功最小;
如图,固定于竖直面内的粗糙斜杆,在水平方向夹角为30°,质量为m的小球套在杆上,在大小不变的拉力作用下,小球沿杆由底端匀速运动到顶端,为使拉力做功最小;