题目内容
一个质量m=2kg的滑块在倾角为θ=37°的固定斜面上，受到一个大小为40N的水平推力F作用，以v0=10m/s的速度沿斜面匀速上滑．（sin37°=0.6，取g=10m/s2）（1）求滑块与斜面间的动摩擦因数；
（2）若滑块运动到A点时立即撤去推力F，求这以后滑块再返回A点经过的时间．
分析：（1）滑块在水平推力作用下沿斜面向上匀速运动，合力为零，根据正交分解法列方程，求解动摩擦因数；
（2）若滑块运动到A点时立即撤去推力F，滑块先向上做匀减速运动，后向下做匀加速运动．根据牛顿第二定律和运动学公式结合求解时间．
（2）若滑块运动到A点时立即撤去推力F，滑块先向上做匀减速运动，后向下做匀加速运动．根据牛顿第二定律和运动学公式结合求解时间．
解答：解：（1）滑块在水平推力作用下沿斜面向上匀速运动时，合力为零，则有
Fcos37°=mgsin37°+μ（mgcos37°+Fsin37°）
代入解得，μ=0.5
（2）撤去F后，滑块上滑过程：
根据牛顿第二定律得：mgsin37°+μmgcos37°=ma1，
得，a1=g（sin37°+μcos37°）
上滑的时间为 t1=
=1s
上滑的位移为 x=
t1=5m
滑块下滑过程：mgsin37°-μmgcos37°=ma2，
得，a2=g（sin37°-μcos37°）
由于下滑与上滑的位移大小相等，则有
x=
a2
解得，t2=
=
s
故 t=t1+t2=（1+
）s
答：
（1）滑块与斜面间的动摩擦因数是0.5；
（2）若滑块运动到A点时立即撤去推力F，这以后滑块再返回A点经过的时间是（1+
）s．
Fcos37°=mgsin37°+μ（mgcos37°+Fsin37°）
代入解得，μ=0.5
（2）撤去F后，滑块上滑过程：
根据牛顿第二定律得：mgsin37°+μmgcos37°=ma1，
得，a1=g（sin37°+μcos37°）
上滑的时间为 t1=
| v0 |
| a1 |
上滑的位移为 x=
| v0 |
| 2 |
滑块下滑过程：mgsin37°-μmgcos37°=ma2，
得，a2=g（sin37°-μcos37°）
由于下滑与上滑的位移大小相等，则有
x=
| 1 |
| 2 |
| t | 2 2 |
解得，t2=
|
| 5 |
故 t=t1+t2=（1+
| 5 |
答：
（1）滑块与斜面间的动摩擦因数是0.5；
（2）若滑块运动到A点时立即撤去推力F，这以后滑块再返回A点经过的时间是（1+
| 5 |
点评：本题分析滑块的受力情况和运动情况是关键，由牛顿第二定律和运动学公式结合是处理动力学问题的基本方法．
练习册系列答案
期末金牌卷系列答案
轻松课堂标准练系列答案
相关题目
如图所示，O1为一根长L=0.4m的绳子系一个质量m=2kg的小球在竖直平面内顺时针做圆周运动的圆心，M为最高点，P为最低点，O2为一个绕其逆时针做匀速圆周运动的圆环的圆心，最高点为Q，圆环边缘上有两点A、B，弧AB所对的圆心角为30°，PQ=3.2m且与两个圆相切，当小球运动到M点时，绳子突然断开，此时圆环上的A点也转到了Q点，经过一段时间后，小球恰好落在了Q点，而此时30°圆心角所对弧AB上的某点（不包含A、B两点）也转到了Q点，期间圆环至少转了一圈，（忽略空气阻力，取g=10m/s2）求：
（2011?东城区模拟）如图所示，一个质量m=2kg的物块放在光滑的水平面上，对其施加一个F=10N的水平拉力，使物块由静止开始做匀加速直线运动．求：
如图所示，质量M=4kg的木板长L=4m，静止在光滑的水平地面上，其水平上表面左端静置一个质量m=2kg的小滑块（可视为质点），小滑块与板间的动摩擦因数μ=0.2．从某时刻开始，用水平力F=10N一直向右拉滑块，使滑块从木板上掉下来．g取10m/s2．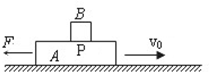
如图所示，木板A长L=6m，质量为M=8kg，在水平面上向右做直线运动．某时刻木板A速度vo=6m/s，在此时刻对木板A施加一个方向水平向左的恒力F=32N，与此同时，将一个质量m=2kg的小物块B轻放在木板A上的P点（小物块可视为质点，放在P点时相对于地面的速度为零），P点到木板A右端距离为lm，木板A与地面间的动摩擦因数为0.16，其他摩擦均不计．取g=10m/s2．求：