题目内容
3. 如图所示,横截面为菱形ABCD的透明体,边长为a,其中∠A=60°,现有一束光线从与A点相距$\frac{a}{4}$处的P点垂直AB射入,如果光线在AD边恰好发生全反射,则
如图所示,横截面为菱形ABCD的透明体,边长为a,其中∠A=60°,现有一束光线从与A点相距$\frac{a}{4}$处的P点垂直AB射入,如果光线在AD边恰好发生全反射,则(1)透明体的折射率为多少?
(2)此光线在透明体中传播的时间为多少?
分析 (1)光线在AD边恰好发生全反射,入射角恰好等于临界角C,由几何关系求出临界角C,再由临界角公式sinC=$\frac{1}{n}$求折射率n.
(2)由几何关系求出光线在透明体中传播的距离,由v=$\frac{c}{n}$求出光线在透明体中传播的速度,即可求得传播时间.
解答  解:(1)光线在AD边恰好发生全反射,入射角恰好等于临界角C,由几何关系得:
解:(1)光线在AD边恰好发生全反射,入射角恰好等于临界角C,由几何关系得:
$\frac{1}{sinC}$=
C=60°
由临界角公式sinC=$\frac{1}{n}$得:
n=$\frac{2\sqrt{3}}{3}$
(2)由几何知识和光的反射定律知,光线射到F点时入射角 i=C=60°,光线在F点发生全反射,并垂直BC边射出.
光线在透明体中传播的距离为:
S=$\frac{a}{4}$tan60°+2(a-$\frac{\frac{a}{4}}{cos60°}$)cos30°+$\frac{a}{4}$tan60°sin60°=$\frac{3a}{8}$(2$\sqrt{3}$+1)
光线在透明体中传播的速度为:v=$\frac{c}{n}$=$\frac{\sqrt{3}}{2}$c
故传播时间为:t=$\frac{S}{v}$=$\frac{(6+\sqrt{3})a}{4c}$
答:(1)透明体的折射率为$\frac{2\sqrt{3}}{3}$.
(2)此光线在透明体中传播的时间为$\frac{(6+\sqrt{3})a}{4c}$.
点评 本题的关键要掌握全反射的条件,由数学知识求出相关角度和光线传播的距离,再结合折射定律研究.

练习册系列答案
相关题目
14.用气垫导轨进行实验时,经常需要使导轨保持水平,检验气垫导轨是否水平的方法之一是,轻推一下滑块,使其先后滑过光电门1和光电门2,如图所示,其上的遮光条将光遮住,电子计时器可自动记录滑块先后经过光电门1、2时的遮光时间△t1和△t2,比较△t1和△t2即可判断导轨是否水平,为使这种检验更精准,正确的措施是( )


| A. | 换用质量更大的滑块 | B. | 换用宽度△x更小的遮光条 | ||
| C. | 提高测量遮光条宽度△x的精确度 | D. | 尽可能增大光电门1、2之间的距离L |
18.下列说法正确的是( )
| A. | 在完全失重的情况下,密闭容器内的气体的压强不为零 | |
| B. | 无论技术怎样改进,热机的效率都不可能达到100% | |
| C. | 气体分子单位时间内与单位面积器壁碰撞的次数与单位体积的分子数和温度有关 | |
| D. | 机械能不可能全部转化为内能,内能也不可能全部转化为机械能 | |
| E. | 凡是不违背能量守恒定律的实验构想,都是能实现的 |
12. 如图所示,空间中的A、B两点分别放置电荷量为+Q和-Q的点电荷,CD是AB连线的中垂线.M、N是关于CD对称的两点,P、N是关于AB对称的两点.则( )
如图所示,空间中的A、B两点分别放置电荷量为+Q和-Q的点电荷,CD是AB连线的中垂线.M、N是关于CD对称的两点,P、N是关于AB对称的两点.则( )
 如图所示,空间中的A、B两点分别放置电荷量为+Q和-Q的点电荷,CD是AB连线的中垂线.M、N是关于CD对称的两点,P、N是关于AB对称的两点.则( )
如图所示,空间中的A、B两点分别放置电荷量为+Q和-Q的点电荷,CD是AB连线的中垂线.M、N是关于CD对称的两点,P、N是关于AB对称的两点.则( )| A. | M、N、P三点的电场强度相同 | |
| B. | M、N、P三点的电势相等 | |
| C. | 将一个负的试探电荷由M点移到P点,试探电荷的电势能增大 | |
| D. | 将一个正的试探电荷由M点移到N点和由M点移到P点,电场力做功相等 |
13.下列说法正确的是( )
| A. | 液体没有一定的形状,能够流动,说明液体分子间的相互作用力和气体分子间的相互作用力一样几乎为零 | |
| B. | 当液体与固体接触时形成的液体薄层叫附着层,该处的液体分子一定比液体内部分子稀疏 | |
| C. | 当液晶中电场强度不同时,它对不同颜色的光的吸收强度不一样,这样就能显示各种颜色,这也是液晶彩电显示屏显示彩色的原理 | |
| D. | 物理学里用空气中的水蒸气的压强与同一温度时水的饱和汽压强的比值来定义空气的相对湿度 | |
| E. | 纸张、棉花、毛巾等物品很容易吸水是因为毛细现象的原因 |
 如图所示,一个圆形线圈的匝数n=1000,线圈面积S=200cm2,线圈的电阻r=1Ω,线圈外接一个阻值R=4Ω的电阻,把线圈放入一方向垂直线圈平面向里的匀强磁场中,磁感应强度随时间变化规律如图所示.求:
如图所示,一个圆形线圈的匝数n=1000,线圈面积S=200cm2,线圈的电阻r=1Ω,线圈外接一个阻值R=4Ω的电阻,把线圈放入一方向垂直线圈平面向里的匀强磁场中,磁感应强度随时间变化规律如图所示.求: 如图所示,厚度d=10cm的矩形玻璃砖与水平实验桌成45°角放置,一激光束平行于水平桌面射到玻璃砖的表面,在桌面上得到两个较亮点A、B,测得A、B间的距离L=10cm,画出形成A、B两个亮点的光路图并求玻璃砖对该激光的折射率.
如图所示,厚度d=10cm的矩形玻璃砖与水平实验桌成45°角放置,一激光束平行于水平桌面射到玻璃砖的表面,在桌面上得到两个较亮点A、B,测得A、B间的距离L=10cm,画出形成A、B两个亮点的光路图并求玻璃砖对该激光的折射率.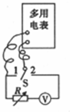 利用图示电路可以测量多用电表内电池的电动势E和欧姆“×100”挡内部电路的总电阻r,提供的器材有:多有电表、电压表(量程3V,内阻几千欧)、电阻箱(0~9999.9Ω)、单刀双掷开关S、导线若干.主要实验步骤如下,请补充完整.
利用图示电路可以测量多用电表内电池的电动势E和欧姆“×100”挡内部电路的总电阻r,提供的器材有:多有电表、电压表(量程3V,内阻几千欧)、电阻箱(0~9999.9Ω)、单刀双掷开关S、导线若干.主要实验步骤如下,请补充完整.