题目内容
11. 如图所示,厚度d=10cm的矩形玻璃砖与水平实验桌成45°角放置,一激光束平行于水平桌面射到玻璃砖的表面,在桌面上得到两个较亮点A、B,测得A、B间的距离L=10cm,画出形成A、B两个亮点的光路图并求玻璃砖对该激光的折射率.
如图所示,厚度d=10cm的矩形玻璃砖与水平实验桌成45°角放置,一激光束平行于水平桌面射到玻璃砖的表面,在桌面上得到两个较亮点A、B,测得A、B间的距离L=10cm,画出形成A、B两个亮点的光路图并求玻璃砖对该激光的折射率.
分析 A亮点是光线在玻璃砖反射形成的.B亮点是光线进入玻璃砖后在左表面反射后,再折射出玻璃砖形成的,根据折射定律作出光路图.
根据几何关系,结合折射定律求出玻璃砖对该激光的折射率.
解答  解:光路图如图所示.由折射定律有:
解:光路图如图所示.由折射定律有:
$\frac{sin45°}{sinγ}$=n
直角三角形MNR中有:
sinγ=$\frac{PN}{2MN}$
则有:MN=$\sqrt{{d}^{2}+(\frac{PN}{2})^{2}}$
在直角三角形PQN中有:PN=$\sqrt{2}$L
解得:n=$\frac{\sqrt{6}}{2}$
答:画出形成A、B两个亮点的光路图如图所示,玻璃砖对该激光的折射率是$\frac{\sqrt{6}}{2}$.
点评 本题的关键理解亮点形成的原因,作出光路图,结合光的折射定律和几何知识解决这类问题,需加强这类题型的训练.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2. 如图所示,甲、乙两物体用压缩的轻质弹簧连接,静置与倾角为θ的粗糙斜面上,稍微增大斜面的倾斜角(甲、乙两物体仍保持静止),下列说法正确的是( )
如图所示,甲、乙两物体用压缩的轻质弹簧连接,静置与倾角为θ的粗糙斜面上,稍微增大斜面的倾斜角(甲、乙两物体仍保持静止),下列说法正确的是( )
 如图所示,甲、乙两物体用压缩的轻质弹簧连接,静置与倾角为θ的粗糙斜面上,稍微增大斜面的倾斜角(甲、乙两物体仍保持静止),下列说法正确的是( )
如图所示,甲、乙两物体用压缩的轻质弹簧连接,静置与倾角为θ的粗糙斜面上,稍微增大斜面的倾斜角(甲、乙两物体仍保持静止),下列说法正确的是( )| A. | 弹簧弹力减小 | B. | 弹簧弹力增大 | ||
| C. | 物体甲所受摩擦力一定减小 | D. | 物体乙所受摩擦力一定增大 |
19.机动车的尾气含有铅等大量有害物质,并且也是造成地球“温室效应”的重要因素之一.电动汽车因其无尾气排放且噪音小等因素,正在逐渐被人们接受.某国产品牌电动汽车的铭牌如下,已知蓄电池储存的电能等于其容量乘输出电压,则下列说法正确的是( )
| 规格 | 后轮驱动直流电动机 |
| 车型:60″电动汽车 | 电动机额定输出功率:1675W |
| 整车质量:400kg | 额定转速:600r/min |
| 蓄电池(容量It=800Ah,输出电压:U≥36V) | 额定工作电压/电流:36V/50A |
| A. | 电动汽车正常工作时消耗的电功率1675W | |
| B. | 电动机的内阻为0.5Ω | |
| C. | 蓄电池充满电后储存的电能不小于2.88×104J | |
| D. | 充满电后在额定功率下连续行驶的时间不小于16h |
16. 据媒体报道,未来的iphone7带有屏幕保护器,保护装置设置在屏幕的4个角落由弹性塑料、聚合物及超薄金属片组成,一旦手机内的加速度计、陀螺仪及位移传感器感知手机掉落,屏幕保护器会自动弹出,并完全吸收手机撞击地面的能量,避免手机屏幕直接接触地面而损坏.已知iphone7s手机设计质量约160g,从1.5m自由掉落,重力加速度g取10m/s2,则以下分析正确的是( )
据媒体报道,未来的iphone7带有屏幕保护器,保护装置设置在屏幕的4个角落由弹性塑料、聚合物及超薄金属片组成,一旦手机内的加速度计、陀螺仪及位移传感器感知手机掉落,屏幕保护器会自动弹出,并完全吸收手机撞击地面的能量,避免手机屏幕直接接触地面而损坏.已知iphone7s手机设计质量约160g,从1.5m自由掉落,重力加速度g取10m/s2,则以下分析正确的是( )
 据媒体报道,未来的iphone7带有屏幕保护器,保护装置设置在屏幕的4个角落由弹性塑料、聚合物及超薄金属片组成,一旦手机内的加速度计、陀螺仪及位移传感器感知手机掉落,屏幕保护器会自动弹出,并完全吸收手机撞击地面的能量,避免手机屏幕直接接触地面而损坏.已知iphone7s手机设计质量约160g,从1.5m自由掉落,重力加速度g取10m/s2,则以下分析正确的是( )
据媒体报道,未来的iphone7带有屏幕保护器,保护装置设置在屏幕的4个角落由弹性塑料、聚合物及超薄金属片组成,一旦手机内的加速度计、陀螺仪及位移传感器感知手机掉落,屏幕保护器会自动弹出,并完全吸收手机撞击地面的能量,避免手机屏幕直接接触地面而损坏.已知iphone7s手机设计质量约160g,从1.5m自由掉落,重力加速度g取10m/s2,则以下分析正确的是( )| A. | 手机落地的速度约为4.5m/s | |
| B. | 保护器弹出的时间应小于0.55s | |
| C. | 手机落地时重力的功率约为7.5W | |
| D. | 若保护器吸收撞击力的时间为0.05s,则地面对手机的平均作用力约为19.1N |
20.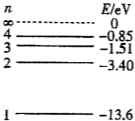 图示为氢原子的能级图.现有大量处于n=4能级的氢原子向低能级跃迁,并辐射出光子.下列说法正确的是( )
图示为氢原子的能级图.现有大量处于n=4能级的氢原子向低能级跃迁,并辐射出光子.下列说法正确的是( )
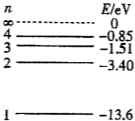 图示为氢原子的能级图.现有大量处于n=4能级的氢原子向低能级跃迁,并辐射出光子.下列说法正确的是( )
图示为氢原子的能级图.现有大量处于n=4能级的氢原子向低能级跃迁,并辐射出光子.下列说法正确的是( )| A. | 该群氢原子向低能级跃迁时,最多可能辐射出6种不同频率的光 | |
| B. | 该群氢原子向低能级路迁时,辐射出光子能量的最大值为0.85eV | |
| C. | 该群氢原子由n=4能级跃迁到n=1能级产生的光频率最高 | |
| D. | 若由n=3能级跃迁到n=2能级产生的光能使某种金属逸出光电子,则由n=2能级跃迁到n=1能级产生的光也一定能使该种金属逸出光电子 | |
| E. | 若由n=4能级跃迁到n=2能级,由n=3能级跃迁到n=2能级和由n=4能级跃迁到n=3能级产生的光的波长分别为λ1、λ2、λ3,则λ1=λ2+λ3 |
 如图甲所示,导体框平面与水平面成θ角,质量为m的导体棒PQ与ab、cd接触良好,回路的总电阻为R,整个装置放置在垂直于框架平面向上,变化磁场中,磁感应强度的大小变化如图乙所示,PQ始终静止,则在0~t0时间内,PQ受到的安培力F、PQ受到的摩擦力f,回路的热功率P、通过PQ的电荷始终静止,则在PQ的电荷量q随时间的变化的图象可能是( )
如图甲所示,导体框平面与水平面成θ角,质量为m的导体棒PQ与ab、cd接触良好,回路的总电阻为R,整个装置放置在垂直于框架平面向上,变化磁场中,磁感应强度的大小变化如图乙所示,PQ始终静止,则在0~t0时间内,PQ受到的安培力F、PQ受到的摩擦力f,回路的热功率P、通过PQ的电荷始终静止,则在PQ的电荷量q随时间的变化的图象可能是( )



 如图所示,横截面为菱形ABCD的透明体,边长为a,其中∠A=60°,现有一束光线从与A点相距$\frac{a}{4}$处的P点垂直AB射入,如果光线在AD边恰好发生全反射,则
如图所示,横截面为菱形ABCD的透明体,边长为a,其中∠A=60°,现有一束光线从与A点相距$\frac{a}{4}$处的P点垂直AB射入,如果光线在AD边恰好发生全反射,则 图中帆板船的帆与船身成37°角,今有垂直于帆,大小为400N的风力作用于帆面上,则船在前进方向上获得的推力为240N,在船的侧面所受的推力为320N.
图中帆板船的帆与船身成37°角,今有垂直于帆,大小为400N的风力作用于帆面上,则船在前进方向上获得的推力为240N,在船的侧面所受的推力为320N.