题目内容
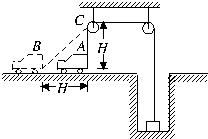
图中,AB=AC=H,开始时绳AC处于竖直方向,小车从静止出发在水平路面上运动到B点时速度为v,在此过程中绳子对挂在井底、质量为m的物体做了多少功?

【答案】
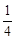 mv2+(
mv2+(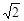 -1)mgH
-1)mgH
【解析】绳子对挂在井底的物体做的功物体克服重力做的功等于物体动能的增加。
将绳末端B的速度v分解为沿绳的速度分量v1和垂直绳的速度分量v2,
如图所示,则井中物体获得的速度等于 v1=v cosθ
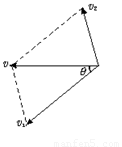
井中物体上升的高度即等于拉过去的绳长,即
h=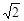 H-H=(
H-H=(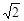 -1)H
-1)H
则由动能定理可得 W -mgh=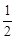 mv12
mv12
得 W=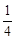 mv2+(
mv2+(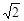 -1)mgH
-1)mgH
思路分析:绳子对挂在井底的物体做的功物体克服重力做的功等于物体动能的增加。根据运动的合成与分解求出井中物体的速度,v1=v
cosθ根据绳长的的变化求出物体上升的高度h=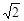 H-H=(
H-H=(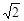 -1)H;最后根据动能定理求拉力做的功。
-1)H;最后根据动能定理求拉力做的功。
试题点评:考查运动的合成与分解问题综合动能定理求解拉力做功问题。综合能力较强,学生易在求速度时出错。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
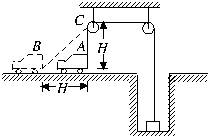 如图,AB=AC=H,开始时绳AC处于竖直方向,物体D通过细绳挂在井底,小车从静止出发,在水平路面上运动到B点时速度为v,求
如图,AB=AC=H,开始时绳AC处于竖直方向,物体D通过细绳挂在井底,小车从静止出发,在水平路面上运动到B点时速度为v,求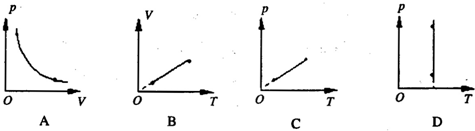



 ,则:
,则:
 ______.已知
______.已知 、
、 、
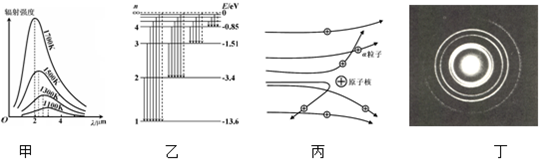
、 和中子的质量分别为m1、m2、m3和m4,则此反应中一个铀核裂变释放的能量为______;
和中子的质量分别为m1、m2、m3和m4,则此反应中一个铀核裂变释放的能量为______;