题目内容
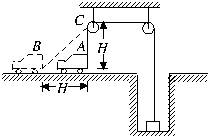 如图,AB=AC=H,开始时绳AC处于竖直方向,物体D通过细绳挂在井底,小车从静止出发,在水平路面上运动到B点时速度为v,求
如图,AB=AC=H,开始时绳AC处于竖直方向,物体D通过细绳挂在井底,小车从静止出发,在水平路面上运动到B点时速度为v,求(1)此时刻悬挂物体D的速度大小,
(2)在此过程中绳子对质量为m的物体D做了多少功?
分析:以质量为m的物体为研究对象.车经过B点时,将车速分解为沿绳子方向和垂直于绳子方向,得到物体m的速度.由几何关系求出此过程物体上升的高度,根据动能定理求解绳子拉力做功.
解答:解:(1)绳子对挂在井底的物体做的功与重力做的功之和等于物体动能的增加.将绳末端B的速度v分解为沿绳的速度分量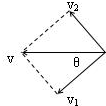 v1和垂直绳的速度分量v2,如图所示,则井中物体获得的速度 v1=vcosθ=vcos45°=
v1和垂直绳的速度分量v2,如图所示,则井中物体获得的速度 v1=vcosθ=vcos45°=
v
(2)井中物体上升的高度即等于拉过去的绳长,即
h=
H-H=(
-1)H
则由动能定理可得
W-mgh=
mv12
得 W=
mv2+(
-1)mgH
答:(1)悬挂物体D的速度大小为
v;
(2)在此过程中绳子对挂在井底的物体做了W=
mv2+(
-1)mgH.
 v1和垂直绳的速度分量v2,如图所示,则井中物体获得的速度 v1=vcosθ=vcos45°=
v1和垂直绳的速度分量v2,如图所示,则井中物体获得的速度 v1=vcosθ=vcos45°=
| ||
| 2 |
(2)井中物体上升的高度即等于拉过去的绳长,即
h=
| 2 |
| 2 |
则由动能定理可得
W-mgh=
| 1 |
| 2 |
得 W=
| 1 |
| 4 |
| 2 |
答:(1)悬挂物体D的速度大小为
| ||
| 2 |
(2)在此过程中绳子对挂在井底的物体做了W=
| 1 |
| 4 |
| 2 |
点评:本题是运用动能定理求变力做功,难点是研究物体的速度与小车的速度关系,运用运动的分解方法.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 (2011?龙岩模拟)如图,AB为一光滑固定轨道,AC为摩擦因素μ=0.25的粗糙水平轨道,D为水平地面上的一点,且B、C、D在同一竖直线上,已知B、C两点的高度差为h,C、D两点的高度差也为h,AC两点相距s=2h.两滑块从A点以相同的初速度v0分别沿两轨道滑行,到达B点或C点后分别水平抛出,欲使两滑块的落地点相同,滑块的初速度v0应满足什么条件?
(2011?龙岩模拟)如图,AB为一光滑固定轨道,AC为摩擦因素μ=0.25的粗糙水平轨道,D为水平地面上的一点,且B、C、D在同一竖直线上,已知B、C两点的高度差为h,C、D两点的高度差也为h,AC两点相距s=2h.两滑块从A点以相同的初速度v0分别沿两轨道滑行,到达B点或C点后分别水平抛出,欲使两滑块的落地点相同,滑块的初速度v0应满足什么条件?
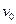 分别沿两轨道滑行,到达B点或C点后分别水平抛出,欲使两滑块的落地点相同,滑块的初速度
分别沿两轨道滑行,到达B点或C点后分别水平抛出,欲使两滑块的落地点相同,滑块的初速度
 分别沿两轨道滑行,到达B点或C点后分别水平抛出,欲使两滑块的落地点相同,滑块的初速度
分别沿两轨道滑行,到达B点或C点后分别水平抛出,欲使两滑块的落地点相同,滑块的初速度